운영관리
Variability and Its Impact on Process Performance
-Waiting Time Problems
개요
- 이번 단원에선 수요가 비정기적으로 도착하는 것이 퍼포먼스에 미치는 영향을 살펴본다.
- 이런 수요의 변동성은 프로세스가 충분한 capacity를 갖고 있다고 해도 고객이 서비스를 받기 위해 대기해야 하는 상황을 만들 수 있다.
- 이 단원에 나오는 프로세스는 Demand < Capacity를 전제로 하기 때문에 Flow rate = Demand로 보아도 무방하다. (원래는 Flow rate = $\min{Demand,\ Capacity}$)
- server가 하나일 경우, 복수일 경우에 대해 살펴볼 것이다.
Variability에 대한 변수
- 기본적으로 Demand, Capacity, Process time, average Inter-arrival time, Average processing time 외에도 다음 변수들을 고려해야 한다.
- Inter-arrival variation
- variation of processing time
Notaton and Basic relations (single server)
- Notation
- $T$ = Flow Time
- $T_q$ = Time in queue
- $p$ = average processing time = Activity time = Service time
- $a$ = average inter-arrival time
- $R$ = Flow Rate
- $I_q$ = Inventory waiting
- $CV_a = \frac{\mathrm{Standard\ deviation\ of\ interarrival\ time}}{\mathrm{Average\ interarrival\ time}}$ = Coefficient of Inter arrival time Variation이 포아송분포를 따른다고 할 때 $CV_a = 1$
- $CV_p = \frac{\mathrm{Standard\ deviation\ of\ activity\ time}}{\mathrm{Average\ activity\ time}}$ = Coefficient of Inter activity time Variation이 포아송분포를 따른다고 할 때 $CV_p = 1$
-
Relations
Little’s Law
- $I = R\times T$
variation과 독립
- Capacity = $1 / p$
- Flow Rate = $\min{\mathrm{Demand, Capacity}} = \mathrm{Demand} = 1/a$
- Utilization = Flow rate / Capacity = $p/a$
variation에 종속
- Flow Time = Time in queue + Service Time $T=T_q+p$
- Inventory = Inventory in process + Inventory in queue $I = I_q\ +\ I_p$
- Inventory in queue = Flow Rate * Time in queue $I_q=R*T_q$
- Inventory in process = Flow Rate * service time $I_p\ =\ R*p\ =\ (1/a)p$
additional Notation and relations (multi-server)
- $m$ = number of servers
- Capacity = $m \times 1/ p$
- Utilization = Flow rate / Capacity = $(1/a)/(m\times1/p)\ \ =\ p/(a\times m)$
Single Server Time in queue
- $\mathrm{Time\ in\ queue = Activity\ Time\ *\ \left({\frac{utilization}{1-utilization}}\right)}\ *\ \left({\frac{CV_a^2\ +\ CV_p^2}{2}}\right)$
Multi-server Time in queue
- $\mathrm{Time\ in\ queue = \left({\frac{Activity\ Time}{m}}\right)\ *\ \left({\frac{utilization^{(\sqrt{2(m+1)}\ \ \ )-1}}{1-utilization}}\right)}\ *\ \left({\frac{CV_a^2\ +\ CV_p^2}{2}}\right)$
Pooling in multiple server condition
- 서버가 여러 개일 때 이들 각각에 queue를 배치하는 것 보다 단일 서버들을 묶어서 하나의 큐로부터 수요를 분배받는게 더 효율적이다. (queue를 공유하자)
- n개의 서버 각각에 queue가 있다면
- a = A * n, p = P, m = 1
- n개의 서버가 하나의 queue를 공유한다면
- a = A, p = P, m = n
Variability and Its Impact on Process Performance
-Throughput Losses
개요
- 이번 단원은 이전 단원의 연장이다.
- 한가지 조건이 바뀌었는데 customer의 인내가 0으로 수렴하여 대기열이 있을 경우 서비스 받기를 거부한다.
- 따라서 Inventory queue는 0이 된다.
- 이전 단원의 전제조건이었던 Capacity > Demand 가 유지된다.
- 이 단원의 중점 사항은 얼마나 많은 수요 Loss가 있을지 예측하는 것이다.
- 이는 Utilization이 1을 넘을 확률을 알면 구할 수 있다.
Notations and basic relations
- Notations
- $m$ : number of server
- $p$ : process time
- $a$ : inter-arrival time
- $P_m(r)$ : probability {All $m$ servers ar busy}
- relations
- $r = \frac{p}{a}$
Flow units lost
= Demand rate * probability that all servers are busy
- $\mathrm{Flow\ units\ Lost = \ }\frac{1}{a} \times P_m(r)$ $(\ \ r = \frac pa\ \ )$
-
Flow rate = Demand rate * Probability that not all servers are busy
$\mathrm{Flow\ rate}\ =\ \frac{1}{a} \times (1-P_m(r))$
Erlang Loss Table
-
Table

-
Formula
$P_m(r)=\frac{\frac{r^m}{m!}}{1+\frac{r^1}{1!}+\frac{r^2}{2!}+…+\frac{r^m}{m!}}$
Quality Management, Stastical Process Control (SPC)
개요
- 프로세스의 생산품의 품질이 정확히 동일하기는 매우 어렵다.
- 기준이 되는 목표 주위로 허용되는 오차가 주워지고, 각 생산품들이 기준에서 얼마나 떨어져 있는지에 대한 수치를 variation이라고 부른다.
- Two types of Variation
- natural variation
- abnormally large variation
- 생산물의 variation은 경향성이 있어서 랜덤하게 왔다갔다 하지 않고 한번 어그러지면 어그러진 쪽으로 계속 variation이 이동한다. 불량품을 하나 생산해낸 프로세스는 차후에 더 많은 불량품을 생산할 가능성이 높아진다는 뜻이다. (이상견빙지)
- 우리가 주목해야 할 것은 생산품의 vatiation이 natural variation 에서 abnormally large variation으로 이동하는 순간을 포착하는 것이 목표이다.
- variation은 각 생산품에 매핑되고, 이때 normal variation에 해당하는 생산품들 간의 variation 격차를 Common Cause Variation이라고 한다. 또한 abnormally large variation에 해당하는 생산품들 간의 variation격차 또한 Common Cause Variation(high level)이다.
- normal variation 생산품과 abnormally large variation 생산품과의 격차는 Assignable cause Variation이라고 한다. 즉 둘 사이의 선을 넘으면 Assignavle cause Variation 이다.
- 따라서 Assignable cause Variation을 찾는 것이 목표가 되겠다.
- natural과 abnormal의 경계
- Upper Control Limit (UCL)
- Lower Control Limit (LCL)
Control Limit의 결정 방법
-
Central Limit Teorum
-
Central Limit Theorum ( CLT, 중심극한정리 )
- Population & Sample
- Population
- 모집단
- 가능한 모든 해의 집합
- Sample
- 표본
- Population 에서 추출한 요소들의 집합
- 관심있는 부류만 추출하는 것도 가능하다.
- Population이 아닌 Sample을 추출하여 사용하는 이유
- 전수조사엔 막대한 비용
- Population에는 적합한 item만 있는게 아니라 고려대상에서 제외된 것들이 있어 선별이 필요.
- 기타 이유로 현실적으로 전수조사가 어려움
- Population
- 모집단과 표본과의 관계
- Population의 mean : $\mu$, variace: $\sigma^2$ 일 때, 여기서 추출한 크기가 $n$인 Sample 을
$\mathrm{x} = {x_1,\ ,x_2\ ,…,x_n}$ 이라고 할때
- $\bar{\mathrm{x}}=\frac{\Sigma_{i=1}^{n} x_i}{n}$
- $\bar{\mathrm{x}}$ 들의 mean $E(\bar{\mathrm{x}})$ $\simeq\mu$
- $\bar{\mathrm{x}}$들의 distribution
$V(\bar{\mathrm{x}})\simeq\frac{\sigma^2}{n}$
- Population의 mean : $\mu$, variace: $\sigma^2$ 일 때, 여기서 추출한 크기가 $n$인 Sample 을
$\mathrm{x} = {x_1,\ ,x_2\ ,…,x_n}$ 이라고 할때
- CLT 개요
- CLT가 강력한 이유는 우리가 모집단의 분산을 알지 못하더라도 충분한 양의 ($n$아니다! $n$은 Sample의 크기) Sample을 보유하고, 표본평균($\bar{\mathrm{x}}$)들을 분석하면 모집단의 평균과 분산의 근사치를 얻을 수 있다. (Sample의 수량이 많을 수록 정확도 상승)
- 위에 나온 엄청난 일이 가능한 이유는 $\frac{(\bar{\mathrm{x}}-\mu)\sqrt{n}}{\sigma}$가 표준정규분포를 추종하기 때문이다.
- 정규분포를 추종하는 집단에서 평균을 중심으로 $\pm3\sigma$의 범위에 임의의 집단의 구성원이 존재할 확률은 99.7%이다.
- 평균을 중심으로 이 $6\sigma$에 걸친 범위 바깥에 존재하는 어떤것은 (잔인하지만) 이 집단의 구성원이 아니라고 보아도 무리가 없다.
- 논리의 확장
- 어떤 집단의 평균을 $\mu$ 분산을 $\sigma^2$이라 할때, 임의의 크기가 n인 표본 $\mathrm{x}$에 대해 표본평균 $\bar{\mathrm{x}}$가 $\left[{\mu-3\frac{\sigma}{\sqrt n},\ \ \mu+3\frac{\sigma}{\sqrt n}}\right]$의 범위에 들지 않는다면 표본 $\mathrm{x}$는 해당 집단의 구성원이 아닐 확률이 99.7%이다.
- 어떤 집단을 normal variation의 집단 이라고 생각해보자
- normal variation에 기대하는 것은 오차범위 이기에 $\mu$는 $\bar{\bar{\mathrm{x}}}\ \ (=E{\bar{\mathrm{x}}})$을 사용한다.
- $\sigma$는 관리자가 설정하는 값이기에 $\frac{\bar{R}}{d_2}$이라는 값을 사용한다.
- 이때 $d_2$는 상수,
$\bar{R} = \max\mathrm{\bar{x}} -\min\mathrm{\bar{x}}$ ($\bar{R}:$ 표본평균의 범위)
- 이때 $d_2$는 상수,
- $\left[{\mu-3\frac{\sigma}{\sqrt n},\ \ \mu+3\frac{\sigma}{\sqrt n}}\right]$ ⇒ $\left[{\bar{\bar{\mathrm{x}}}-3\frac{\bar{R}}{d_2\sqrt n},\ \ \bar{\bar{\mathrm{x}}}+3\frac{\bar{R}}{d_2\sqrt n}}\right]$
- $\frac{3}{d_2\sqrt{n}} = A_2$로 간소화 한다. (n에 따라 달라지는 상수)
- $\left[{\bar{\bar{\mathrm{x}}}-3\frac{\bar{R}}{d_2\sqrt n},\ \ \bar{\bar{\mathrm{x}}}+3\frac{\bar{R}}{d_2\sqrt n}}\right]$ ⇒ $\left[{\bar{\bar{\mathrm{x}}}-A_2\bar{R}\,\ \ \bar{\bar{\mathrm{x}}}+A_2\bar{R}}\right]$
- 결국 문제를 풀 때 $A_2$는 교제에 주어지고, 표본평균들의 평균을 구하여 $\bar{\bar{\mathrm{x}}}$를 만들고, 표본평균들의 최대 최소값의 차이인 $\bar{R}$을 구하면 손쉽게 normal variation집단의 범위를 구할 수 있다.
- 어떤 집단을 normal variation의 집단 이라고 생각해보자
- 어떤 집단의 평균을 $\mu$ 분산을 $\sigma^2$이라 할때, 임의의 크기가 n인 표본 $\mathrm{x}$에 대해 표본평균 $\bar{\mathrm{x}}$가 $\left[{\mu-3\frac{\sigma}{\sqrt n},\ \ \mu+3\frac{\sigma}{\sqrt n}}\right]$의 범위에 들지 않는다면 표본 $\mathrm{x}$는 해당 집단의 구성원이 아닐 확률이 99.7%이다.
- Population & Sample
Control Limit의 결정 방법
-
$p-\mathrm{Chart}$
-
$p-\mathrm{Chart}$
- 증명없이 사용한다.
- Mean Proportion Defective $p$ $p=\frac{\mathrm{Total\ number\ defective}}{\mathrm{Total\ number\ of\ items\ sampled}}$
- Standard Error of the Sample Proportion $S_p$ $S_p=\sqrt{\frac {p(1-p)}{n}}$
- Control Limits for Proportions $\mathrm{UCL,\ LCL}$ $\mathrm{UCL,\ LCL} = p\pm3\sqrt{\frac {p(1-p)}{n}}$
Specification & Control limits
- 용어 정의
-
Specifications (Tolerance)
engineering design을 고려해 정한(관측된이 아니다) 품질 허용 범위
Ex) Specification of acceptable item USL = Upper Specification Limits LSL = Lower Specification Limits
-
Control Limits
생산된 샘플을 보고 도출해 낸 Statistical limits으로 관측의 결과가 된다.
-
Process Variability
Control Limits에 직접적으로 영향을 받으며 Specification과 독립이다.
Process Variability = UCL - LCL
-
- Specification 과 Control Limits(Process variability) 의 세 가지 관계
-
A. Process variability matches Specifications
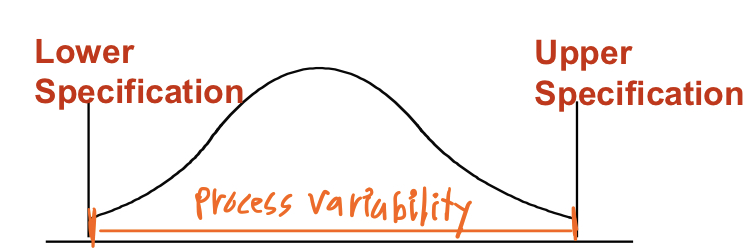
-
B. Process Variability well within specifications
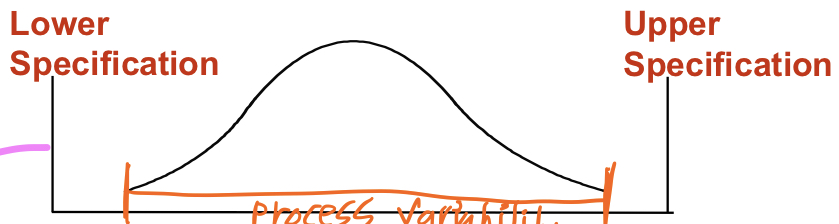
-
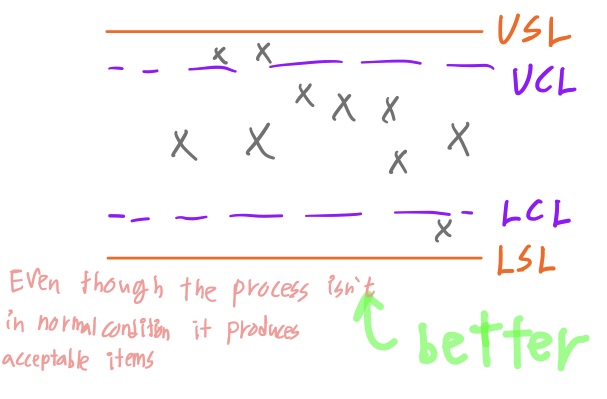
C. Process Variability exceds specifications
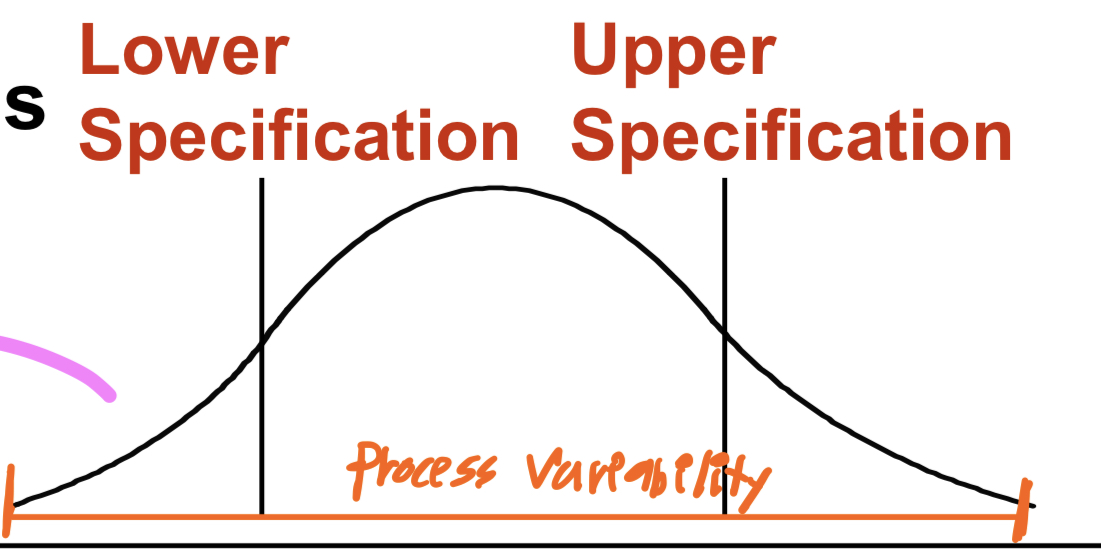
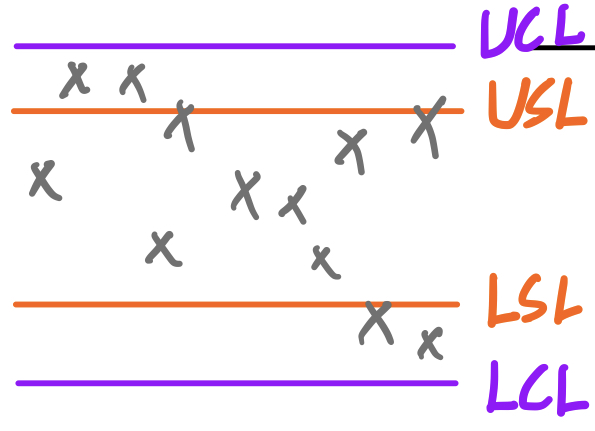
→ Even though the process is in control it produce defective units
-
Process Capability
-
Process와 Specification의 mean이 동일할 때 Process Centered 상태라고 한다.
이 때 Process capability ratio 를 $C_p$로 표기한다.
$C_p = \frac{\mathrm{Specification\ width}}{\mathrm{process\ width}} = \frac{\mathrm{Upper\ specification - Lower\ specification}}{6\sigma}$
-
둘의 mean이 일치하지 않을 땐 $C_{pk}$를 사용한다.
$C_{pk}=\min\left({\frac{\bar{\mathrm{x}}-\mathrm{LSL}}{3\sigma},\ \frac{\mathrm{USL}-\bar{\mathrm{x}}}{3\sigma}}\right)$
$\bar{\mathrm{x}}$는 프로세스의 Mean이다.
- $C_p$ 또는 $C_{pk}$가 1보다 크다면 프로세스는 Capable 하다고 판단한다. (세가지 관계 중 A, B에 속함) 작다면, Incapable하다고 판단할 수 있다. (세가지 관계 중 C에 속함)
- Control limits와 Specification Limits를 혼동하지 말것
- 프로세스는 Control 상태일지라도 (spec에)Incapable 할 수 있으며
- out of Control이더라도 Capable할 수 있다.
Forecasting
개요
- Forecasting 이란?
- A statement about the { future value of a { variable of interest } }
- A tool used for predicting { future demand based on { past demand information } }
- 여기선 수요 예측이라 할 수 있다. predict of demand
- Forecasting 의 효용
- Strategic planning ( long range planning )
- Finance and accounting ( budgets and cost controls )
- Marketing ( future sales, new products )
- Production and operations
- Forecasts의 features
- 과거 사건의 데이터로 미래를 예측하는것
- randomness 요소가 많아 정확한 예측은 불가능
- 한가지 특정 요소에 대한 예측보단 그룹에 대한 예측이 더 정확하다.
- 현재로부터 시간이 멀어질 수록 예측의 정확성은 감소한다.
Steps in Forecasting Process
- Determine purpose of forecast
- Establish a time horizon
- Select a forecasting technique
- Obtain, clean and analyze data
- Make the forecast
- Monitor the forecast
Types of Forecasts
- Judgemental: uses subjective inputs
- 주관적 정보를 이용한 예측 (Ex. consumer surveys)
- Time series: uses historical data, assuming the future will be like the past
- 과거 사건을 기반으로 미래를 예측
- Associative models: uses explanatory variables to predict the future
- 대상과 연관된 변수들을 조합하여 미래를 예측
Types of Forecasts
-
Time Series Forecast 상세
- Trend: long-term movement in data
- Cycles: wavelike variations of more than one year’s duration
- 총선시기, 대선시기, 올림픽시즌
- Seasonality: short-term regular variations in data
- Calendar or time of day
- 음식점의 점심시간 수요, 저녁 시간 수요 의 주기성
- Calendar or time of day
- Irregular variations: caused by unusual circumstances
- 파업, 기상 변동
- Random variations: caused by chance
- COVID-19
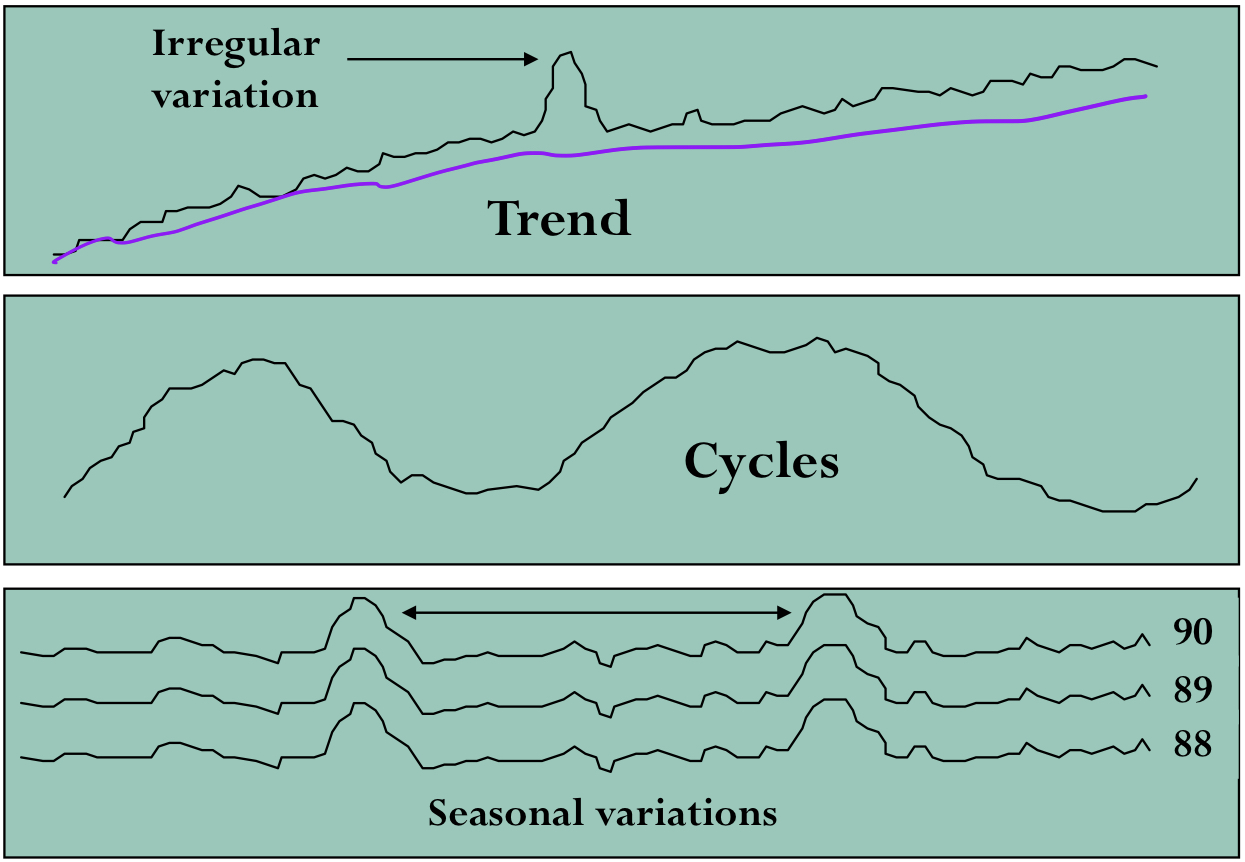
Naive Forecasts
- forecast for any period equals the previous period’s actual value
- 당기의 전망은 전기의 관측 데이터와 정확히 일치할 것이다라는 예측
- Notations & Relations
- Notation
- $F(t)$ : Forecast for time t
- $A(t)$: Actual value of a variable at time t
- Relations
-
Stable time series data 가정
$F(t) = A(t-1)$
-
Seasonal variations 상황 가정
$F(t) = A(t-n)$ (n은 season 주기)
-
Data with trends 상황 가정
$F(t)=A(t-1)+(\ A(t-1)-A(t-2)\ )$
(일정한 기울기)
-
- Notation
Techniques for Averaging
- Notations
- Moving average
- $\mathrm{F_t}$ : Forecast for time period t
- $\mathrm{MA_n}$ : n period moving average
- $\mathrm{A_{t-1}}$ : Actual in period t-1
- $\mathrm{n}$ : Number of periods (data points) in the moving average
- Weighted Moving Averages
- $\mathrm{WMA_n}$ : n period weighted moving average
- $\mathrm{W_i}$ : Weight $(\mathrm{W_1+W_2+…+W_n=1})$
- Exponential Smooting
- $\alpha$: Smoothng Constant
- Moving average
- Moving average
-
Recent Actual values들을 이용해 평균을 내는 방법, 새로운 Actual value가 추가될 때 마다 업데이트를 해주어야 한다.
$\mathrm{F_t = MA_n=\frac{A_{t-n}+…+A_{t-2}+A_{t-1}}{n}}$ (최근 n년간의 Moving average)
-
- Weighted moving average
-
최신의 관측치 일수록 더 높은 가중치를 주어 최신의 데이터의 영향력 제고
$\mathrm{F_t = WMA_n=W_nA_{t-n}+…+W_2A_{t-2}+W_1A_{t-1}}$
-
- Exponential smoothing
-
각 기의 예측들은 전기의 예측치에 전기 예측 오차의 $\alpha$배 만큼을 더하여 산정한다.
Next forecast = previous forecast + $\alpha$(Actual - prev forecast)
$\mathrm{F_t=F_{t-1}+}\alpha(\mathrm{A_{t-1}-F_{t-1}})$
-
Linear Trend Equation
- Notation
- $\mathrm{F_t}$ : Forecast for period t
- $\mathrm{t}$ : Specified number of time periods
- $\mathrm{a}$ : Value of $\mathrm{F_t}$ at $\mathrm{t=0}$
- $\mathrm{b}$ : Slope of the line
- $\mathrm{F_t=a+bt}$
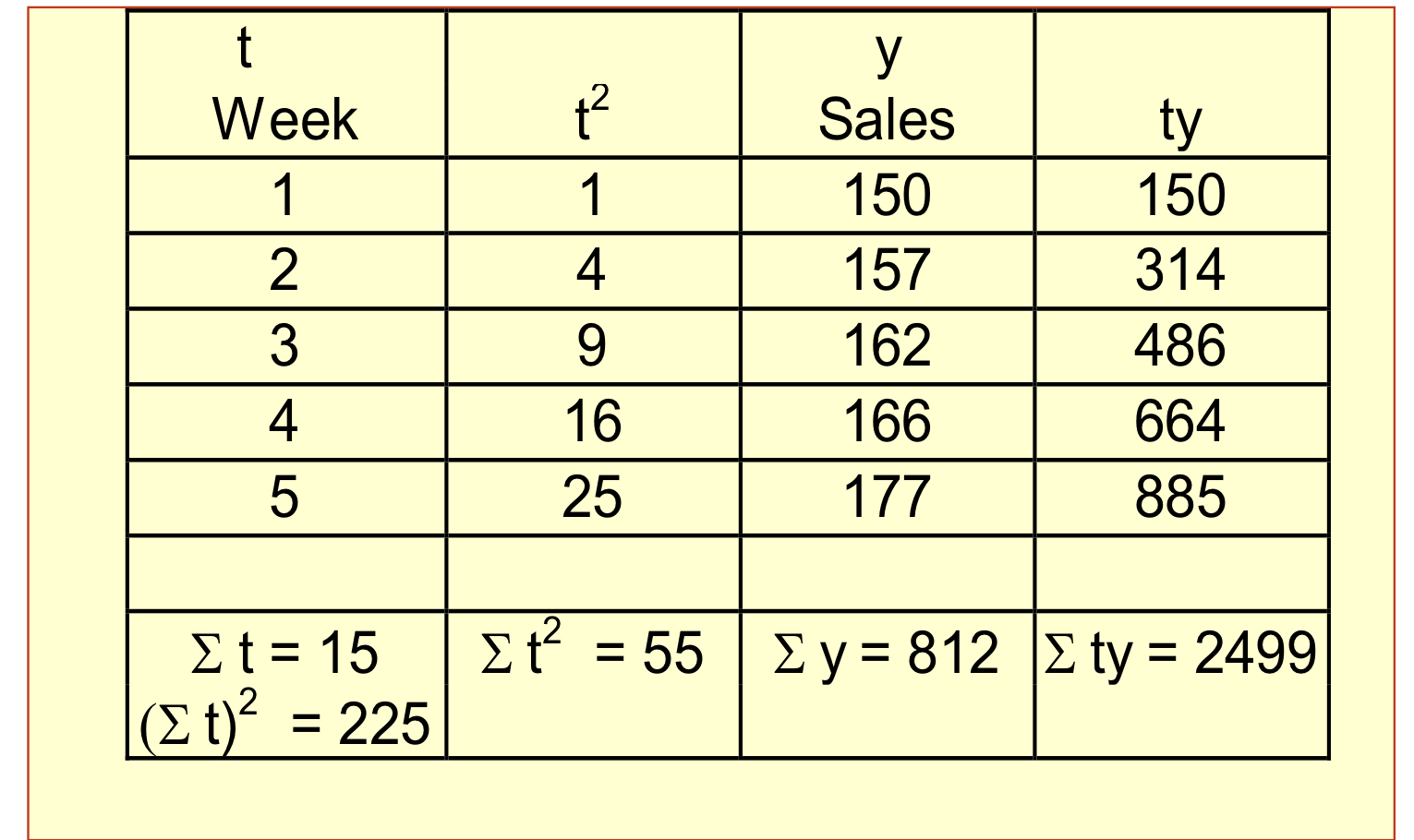
- $\mathrm{b=\frac{n\Sigma(ty)-\Sigma t\Sigma y}{n\Sigma t^2 - (\Sigma t)^2}}$
- $\mathrm{a = \frac{\Sigma y - b\Sigma t}{n}}$
-
예제
y와 t가 문제에서 주어지면 Linear Trend Equation을 산출하는게 문제
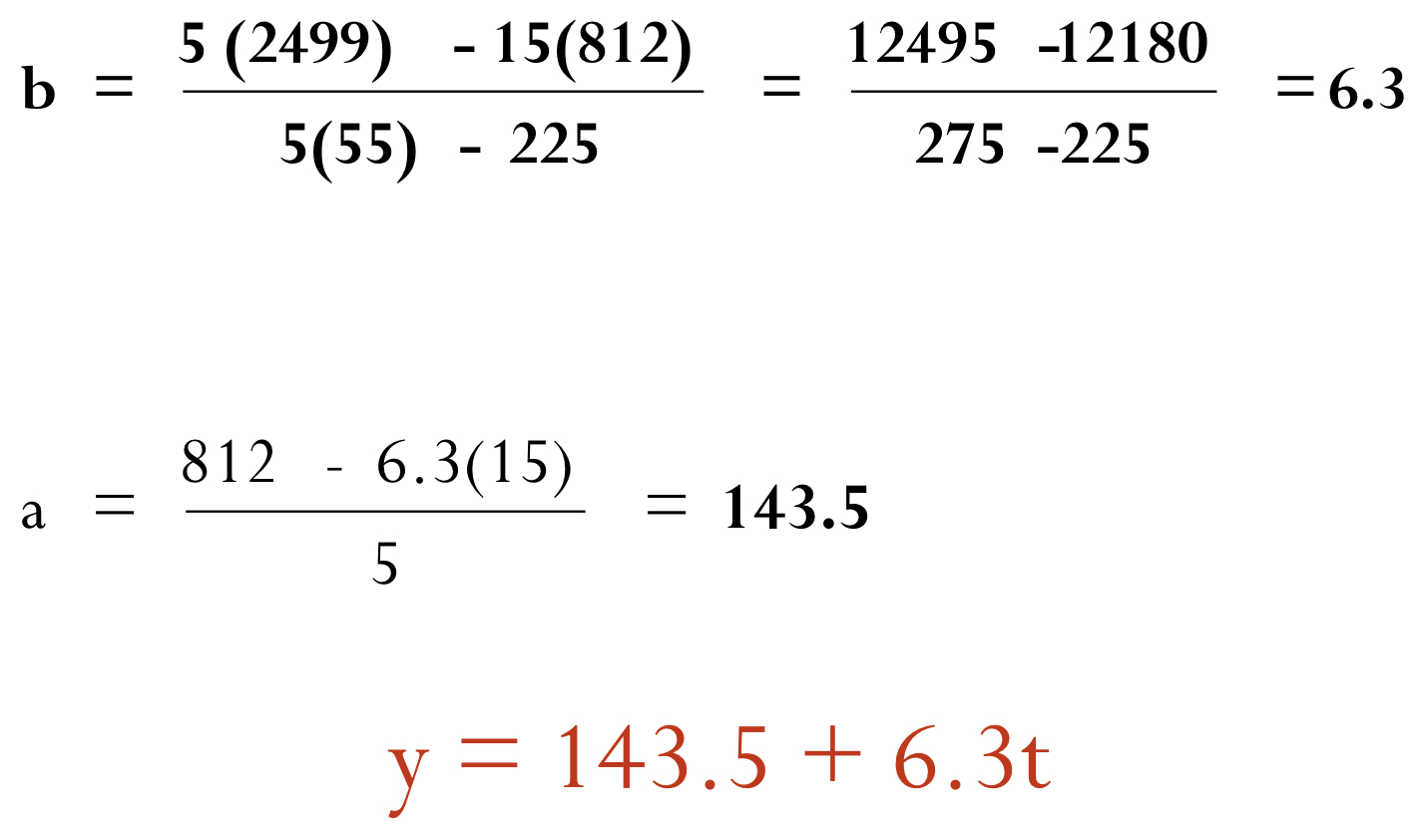
Forecast Accuracy (MAD, MSE)
- 용어 정리
- Error: difference between actual value and predicted value
-
Mean Absolute Deviation (MAD)
Average absolute error $ $ $\mathrm{MAD=\frac{\Sigma\ |\ Actual-forecast\ |\ }{n}}$
- Weights errors linearly
-
Mean Squared Error (MSE)
Average of squared error
$\mathrm{MSE=\frac{\Sigma\ (Actual-forecast)^2\ }{n}}$
- More weight to large errors
Scheduling
개요
- Scheduling 이란?
- Establishing the timing of the use of equipment, facilities, and human activities
- Scheduling의 효용
- Cost savings
- Increases in productivity
- reduces Throughput Losses
- 두가지 중점 사안
-
Loading
일을 어디에 배치하는가
-
Sequencing
어떤 순서로 일을 처리하는가 -priority rules
-
Loading
- 투입요소와 산출요소
- Inputs
- Controllable Inputs ( Decision Variables )
- Uncontrollable Inputs ( Environmental Factors )
- output ( Project Results)
- Mathematical Model
- Inputs 를 Outputs로 변환하는 수학식
-
개략도
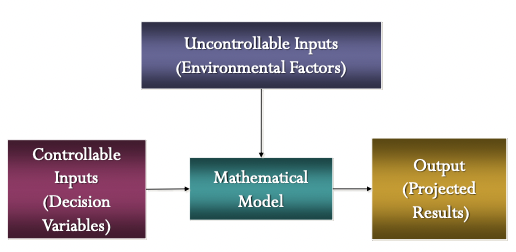
- Inputs
- Linear Programming(LP) Problem
- objective
- 해 들을 평가하는 기준으로 해가 갖는 어떤 특성이 최대한 충족해야할 조건에 대한 표현
- feasible solution
- 모든 제약들을 만족하는 해
- optimal solution
- feasible solution 중 objective를 충족하는 최적의 해
- objective
- LP 조건하 Loading Formulation
- Notation
- $\mathrm{x_{ij}}=\begin{cases}1&\mathrm{if\ agent\ i\ is\ assigned\ to\ task\ j} \ 0 &\mathrm{otherwise}\end{cases}$
- $\mathrm{c_{ij}}=\mathrm{cost\ of\ assigning\ agent\ i\ to\ task\ j}$
-
Formulation
$\mathrm{Min\ \Sigma_i(\Sigma_jc_{ij}x_{ij})}$
$\mathrm{s.t.\ \ \Sigma_jx_{ij}=1\ \ for\ each\ agent\ i}$
$\mathrm{\ \ \ \ \ \ \ \Sigma_ix_{ij}=1\ \ for\ each\ agent\ j}$
$\mathrm{\ \ \ \ \ \ \ x_{ij}=0\ or\ 1\ \ for\ all\ i\ and\ j}$
-
예제
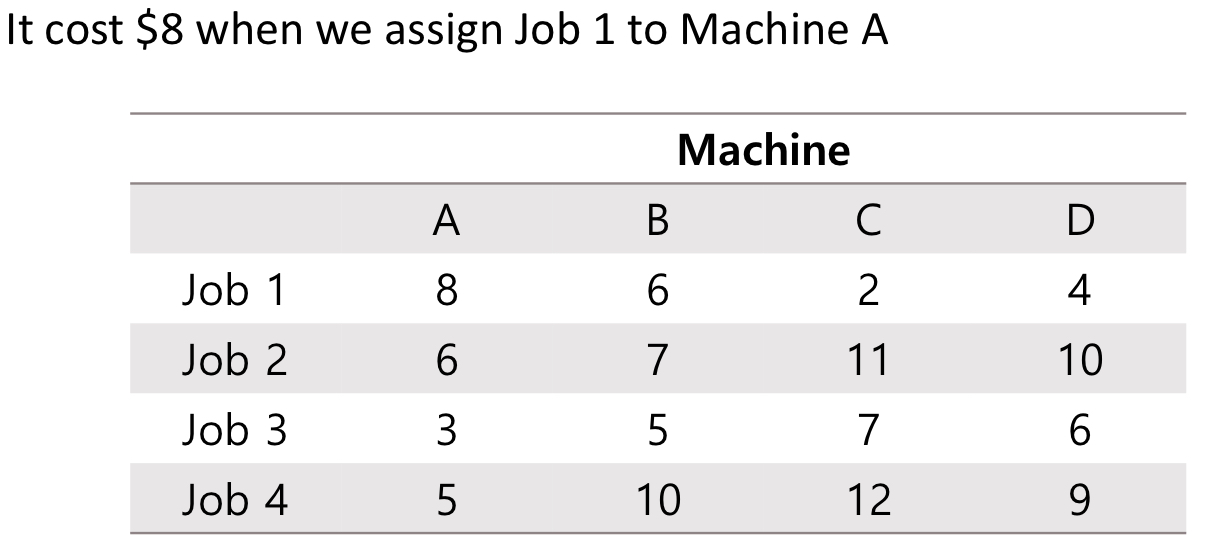
Formulation
Min{$\mathrm{8x_{A1}+6x_{B1}+2x_{C1}+4x_{D1}}$
$\mathrm{+6x_{A2}+7x_{B2}+11x_{C2}+10x_{D2}}$
$\mathrm{+3x_{A3}+5x_{B3}+7x_{C3}+6x_{D3}}$
$\mathrm{+5x_{A4}+10x_{B4}+21x_{C4}+9x_{D4}}$}
- Notation
Sequencing
- 개요
- Priority rules
- Simple heuristics used to select the order in which jobs will be processed
- Job Time
- Time needed for setup and processing of a job
- Priority rules
- Priority Rules
- 종류
- FCFS: First Come First Served
- SPT: shortest processing time
- EDD: earliest due date
- CR: Critical ratio
- Critical = (remaining time) / (process time)
- remaining time can be minus
- Rush: emergency or preferred customers first
- 측정기준
- Job flow time
- 하나의 작업(일)이 처리되기까지 소요시간
- 대기시간을 포함한다.
- Job lateness
- lateness = (Completion time) - (due date)
- tardiness = lateness (if lateness < 0 → tardiness = 0)
- Makespan
- 모든 일을 처리하기까지 소요되는 시간
- 첫 job의 processing이 시작될 때부터 마지막 job이 끝날 때까지 시간간격
- Average number of jobs
- Total flow time / Makespan
- makespan의 기간에 처리되지 않은 작업의 평균 개수
- Job flow time
- 예제
-
problem
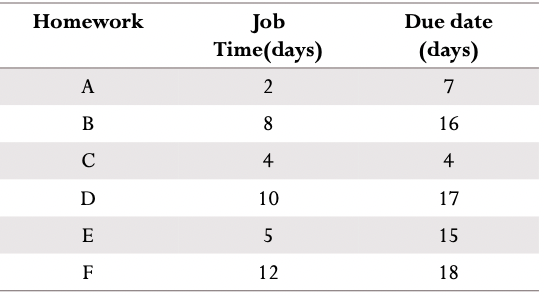
-
SOL
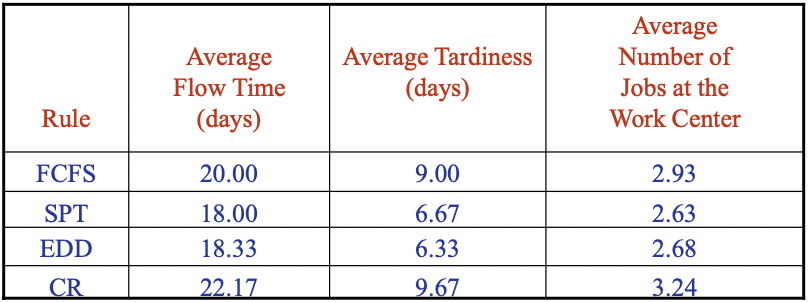
-
- 종류
Johnson’s Rule
- 사용 조건
- 모든 작업 시간은 각각 독립이고, 확정적이어야 한다.
- 선행작업이나 후행작업 등의 관계가 설정되어 있지 않아야 한다.
- 작업은 모두 2개의 work center를 거쳐 완제품이 되어야 한다.
- 각 작업이 거치는 work center의 순서는 동일해야 한다.
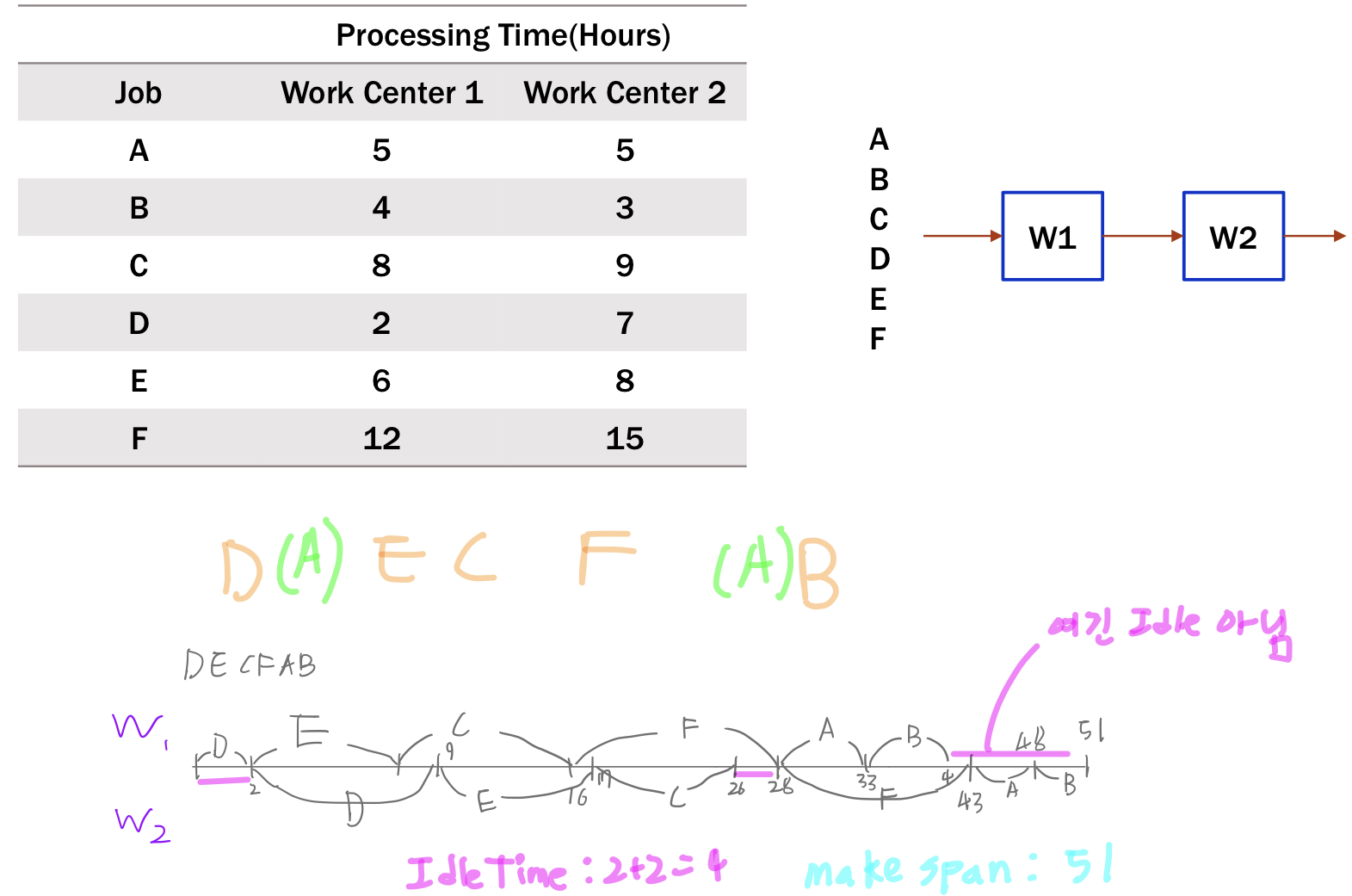
- Johnson’s Rule Optimum Sequence
- 모든 작업을 Work Center의 종류에 관계 없이 둘중 작은 processing time을 산출한다.
- 산출한 결과를 바탕으로 정렬한다.
- 정렬된 job list에서 작은 processing time을 갖는 job을 꺼낸다.
- job 의 processing time이 속한 Work Center에 따라 다음을 진행한다. a. WC1일 경우 sequence list 앞에서부터 쌓아 올린다. b. WC2일 경우 sequence list 뒤에서부터 쌓아올린다.
- job list가 empty일 때까지 3, 4를 진행한다.
-
예제
Aggregate Planning
개요
- Aggregate Planning 이란?
-
중기적인 capacity planning (2 ~ 12개월 앞의 미래를 뜻한다.)
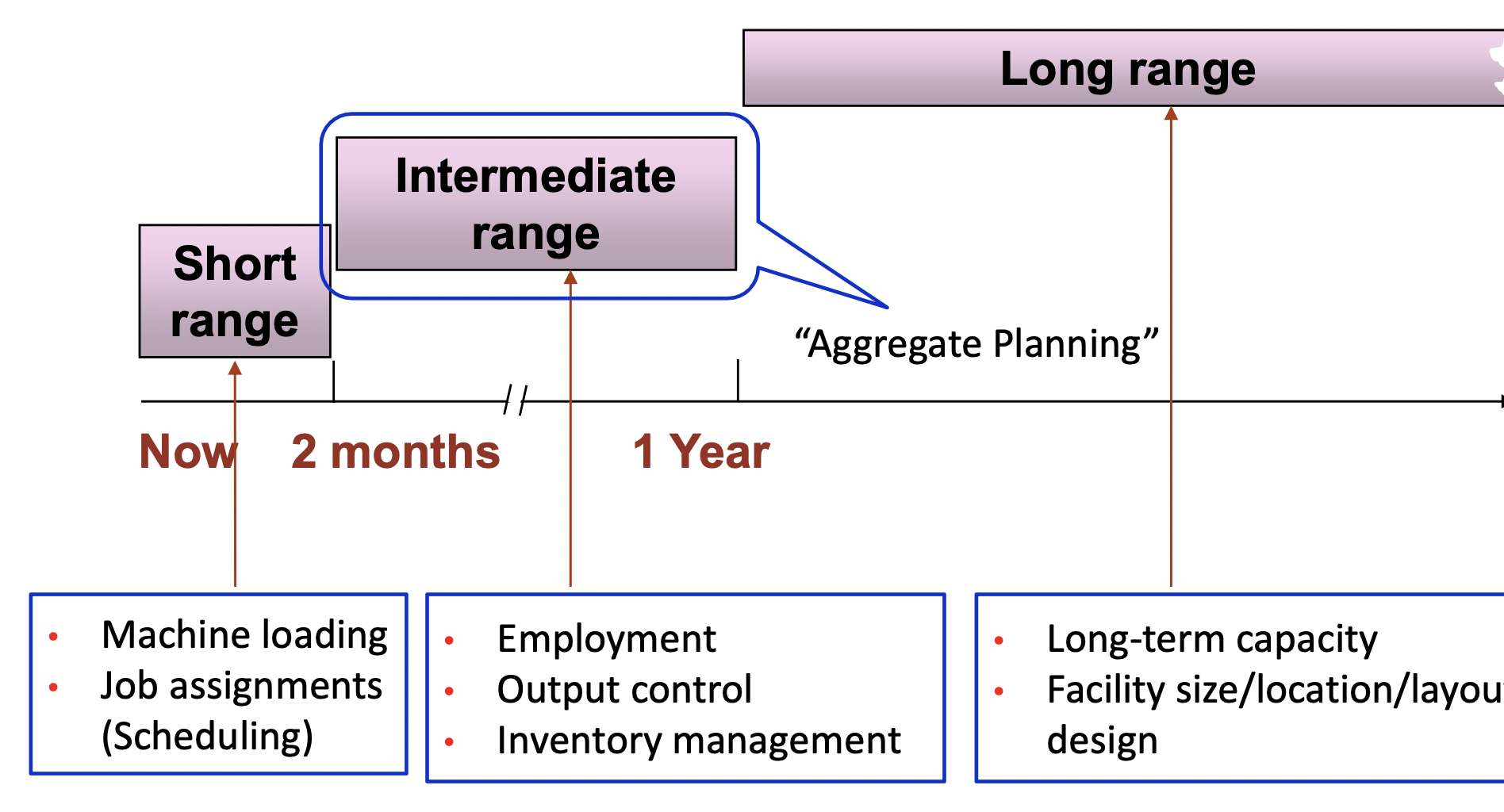
-
특정 모델의 생산에 대한 계획을 짜는 것이 아니라 어떤 제품군의 생산을 계획하는 것
Ex. 현대 모터스: 아반떼 100대, 소나타 100대, … → X 승용차 1000대, 트럭 200대,…. → O
-
- 조정 요소
- Proactive : alter demand to match capacity (능동적으로 demand 조정)
-
Pricing
Ex. 조조할인을 통한 수요 분산
-
Promotion
Ex. 블랙프라이데이 세일을 이용한 비선호품 수요 증가 재고처리,
-
Back orders
수요가 감당 못하게 많을 때 대기열을 생성하여 수요 소폭 하향, 납품 기한 연장
-
New demand
신체품 출시로 새로운 수요를 창조
-
- Reactive: alter capacity to match demand ← 이것에 초점을 두고 본다.
- Hire and lay off worker (고용, 해고)
- Overtime / slack time (초과근무, 납품지연)
- Part-time workers (아르바이트)
- Inventories (재고 관리)
- Subcontracting (하청)
- Proactive : alter demand to match capacity (능동적으로 demand 조정)
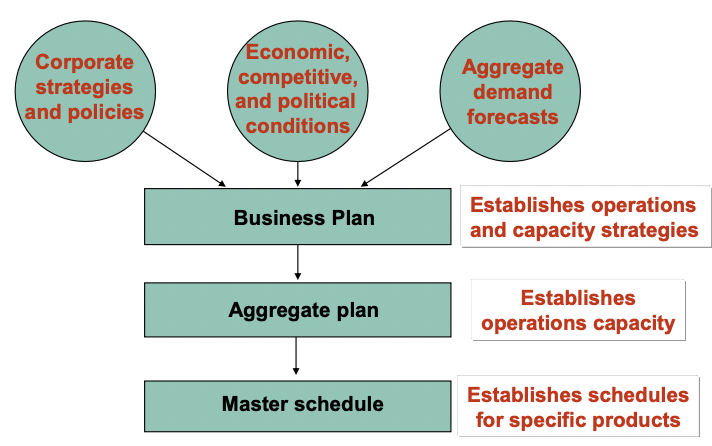
- Production plan은 aggregate planning의 결과물이다.
- Plan을 주기적으로 업데이트 해주어야 한다.
- 12 - 18개월 앞을 항상 내다 볼 수 있도록 최신화 시켜주어야 한다.
Aggregate Planning Inputs
- Resources
- Workforce
- Facilities
- Costs
- Inventory carrying
- Back orders
- Hiring/Fireing
- Overtime
- Inventory changes
- Subcontracting
- Demand forecast
- Policies
- Subcontracting (how much /N)
- Overtime (how much /N)
- Inventory levels (how much / N)
- Back orders (how much /N)
Aggregate Planning outputs
- Total Cost of a plan
- Projected levels of
- Inventory
- output
- Employment
- Subcontracting
- Backordering
Basic Strategies
-
상황 제시

-
사용 전략
-
Level capacity strategy

- 정상 작업시간 내의 생산역량을 일정하게 유지하는 전략
- 실 수요에 따라서 policies에 입각해 대처
- 장점 안정적인 생산역량 유지
- 단점 재고 비용이 증가할 수 있음 초과근무비용, idle time 이 증가할 수 있다. utilization이 낮아질 수 있다.
-
Chase demand strategy
- 수요에 맞게 생산역량(capacity)을 그때그때 조정
- Forecast와 planned output은 세트로 움직인다.
- 장점 재고비용 감소 utilization 이 높게 유지됨(+보통 고용보단, overtime을 사용)
- 단점 생산량 또는 노동력을 조정하는데 드는 비용이 높다.
-
Relations
- Number of workers in a period = Num of workers at end of prev period + Number of new workers at start of period - Number of laid-off workers at start of the period
- Inventory at the end of a period = Inventory at the end of the previous period + production in the current period - Amount used to satisfy demand in the current period
- Average inventory = $\mathrm{\frac{Beginning\ inventory+Ending\ inventory}{2}}$
- Cost for a period = Output cost + Hire/lay-off cost + Inventory cost + Back-order cost *Output cost = Regular work cost + Overtime cost + Subcontract cost
Material requirements planning (MRP)
개요
- 최종 생산물을 만들기 위해 여러 반제품들이 필요한 생산 공정의 Planning
-
개략도
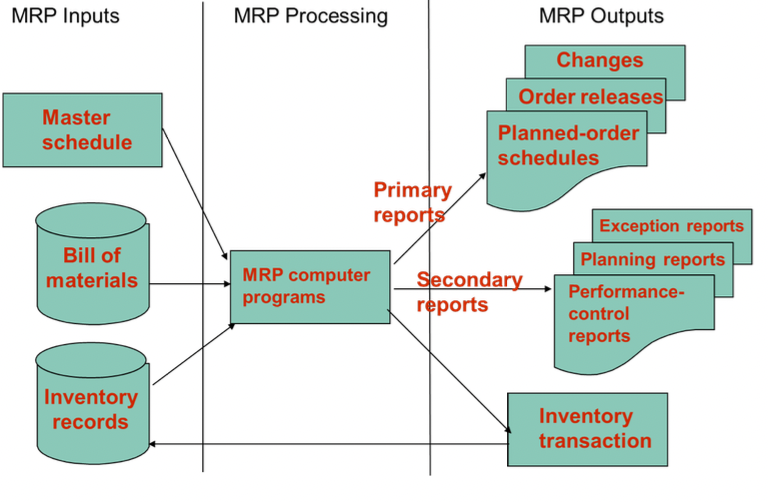
Inputs
- Master Schedule
- 어떤 제품/반제품이 언제까지 얼마나 생산되어야 하는지에 대한 문서
-
예시
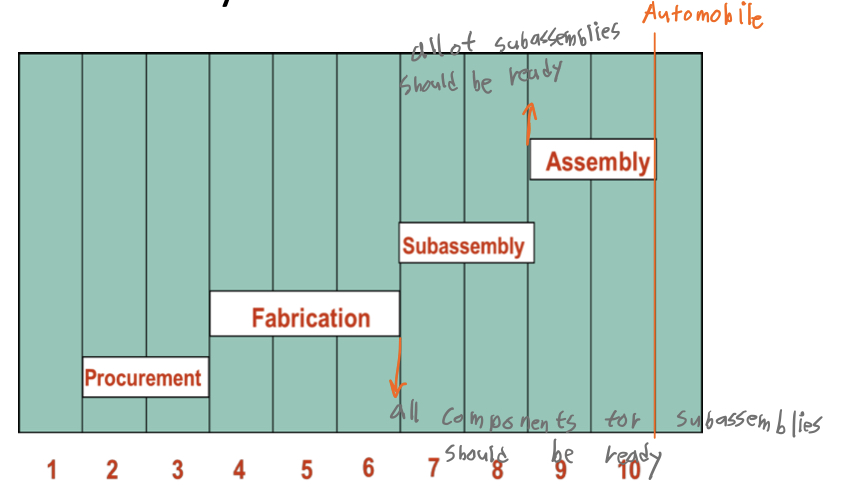
-
cumulative lead time
모든 요소들의 lead time (조달기한) 의 누적
- Bill of materials (BOM)
- 최종 생산물의 완성에 필요한 모든 원제료, 부속 그리고 조립 공정까지에 대해 적힌 명세서
- Product structure tree
-
BOM을 tree 형태로 시각화 한 것
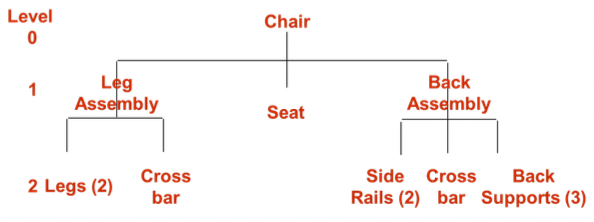
-
- Inventory Records
- 다음의 item에 대해 기한과 함께 명시해 놓은것
- Gross requirements
- Scheduled receipts
- Amount on hand
- Lead times
- Lot size
- etc…
- Net requirements = Gross req - available Inventory
- Available Inventory = Projected on hand - Safety stock - Inventory allocated to other items *이 단원 내에서 safety stock과 inventory allocated to othre items 는 0으로 가정
-
예시
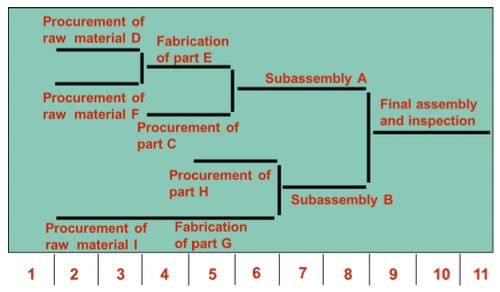
- 다음의 item에 대해 기한과 함께 명시해 놓은것
개념 간단 정리
- Gross requirements
- Total expected demand for an item during each time period without regard to the amount on hand
- 내가 지금 몇개 가지고 있는지와 관계 없이 해당 기간 내에 필요한 item의 수량
- 어떤 생산물 A을 생산하기 위한 부속 b의 경우 A의 planned-order releases에서 정보를 얻을 수 있다.
- Scheduled receipts
- Open orders scheduled to arrive from vendors or elsewhere by the beginning of a period
- 해당 기간 시작일에 예약으로 들어온 item 수량
- Planned on hand
- 어떤 기간의 시작일에 내가 보유하고 있을 것으로 예상되는 item 수량
- = 전기의 Scheduled receipts + 전기의 available inventory
- Net requirements
- Gross - inventory we have
- Planned-order receipts
- Quantity expected to received at the beginning of the period
- 해당 기간 초까지 생산 완료 되어야 할 수량
- Planned-order releases
- 해당 기간에 초까지 생산 준비 되어야 할 수량 (준비되어야 할 반제품들의 세트)
- Planned-order releases = Planned-order receipts / (1-불량률) 불량률은 아직 고려 안하니 둘을 같다고 보면된다.
- 해당 기간에 초까지 생산 준비 되어야 할 수량 (준비되어야 할 반제품들의 세트)
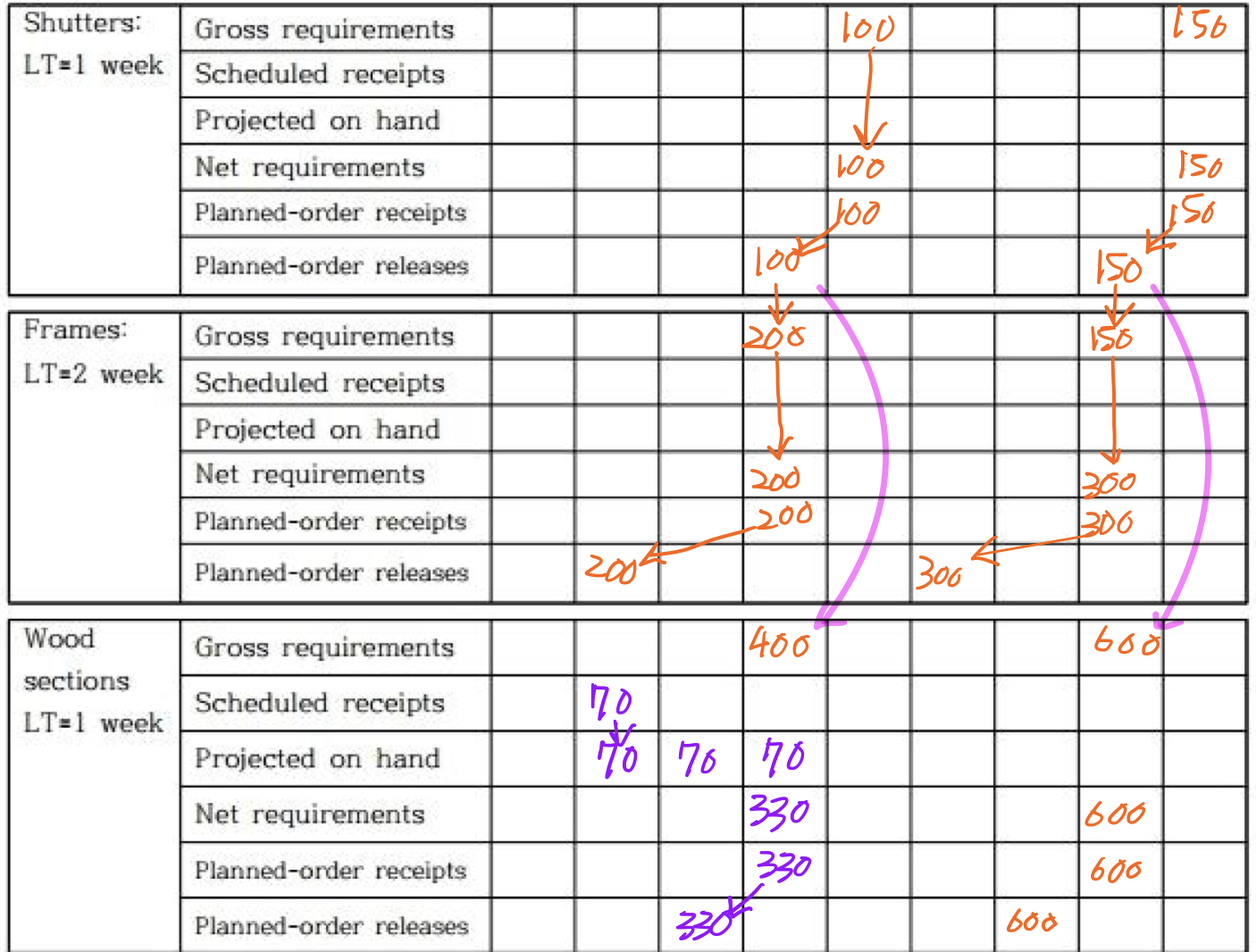
table 예시
-
Master schedule

- Shutter = Frame(2) + Wood section(4)
-
Table

There are currently no comments on this article
Please be the first to add one below :)
내용에 대한 의견, 블로그 UI 개선, 잡담까지 모든 종류의 댓글 환영합니다!!