Artificial Intelligience
9. Goal reduction
문제축소란?
문제를 묘사할 때 문제 축소 연산자를 이용해 부분 문제(Sub goal)으로 분할하는 과정
궁극적으로 해가 분명한 원시문제들로 변환시키는 것
(이 때 최대한 축소하여 생성된 단위 문제가 풀리지도, 더이상 쪼개지지도 않는다면 다른 방법을 시도해보거나 그것도 안된다면 풀리지 않는 문제로 분류된다.)
문제 묘사의 세가지 구성요소 (S, F, G)
- 출발 상태들의 조합: S (start)
- 상태묘사를 다른 상태묘사로 변환시키는 연산자 조합: F (function)
- 목표상태의 조합: G (goal)
문제 축소 기법
- 생태공간 탐색문제를 보다 간단한 탐색 문제로 연속적으로 축소하는 방법
- 문제 분리의 기점 문제 분리의 기점이 되는 상태들을 g1, g2 … , gn이라고 할 때 초기 문제를 (S, F, {g1}), ({g1}, F, {G2}), … , ({gn}, F, G) 문제들의 조합으로 축소
- 키 연산자의 발견
문제 해결에 중요한 단계인 키 연산자를 얻는다면 문제 축소의 주요 기점 gx로 활용
-
차이를 이용한 문제 축소 기법
키 연산자의 후보가 될 수 있는 것을 구하는 한 가지 방법으로 출발노드 집합의 원소들과 목표노드 집합의 원소와의 차이를 이용하는 방법
예시 <원숭이 바나나="" 문제=""> 상태묘사 스키마: **(w, x, y, z)**
w = 원숭이의 수평위치 (2차원 벡터)
x = 원숭이가 상자 위에 있는지 여부 (상자 위: 1, 아니면 0)
y = 상자의 수평 위치 (2차원 벡터)
z = 원숭이가 바나나를 잡았는지 (잡았으면 1, 아니면 0)
S = (A, 0, B, 0) , G = (C, 1, C, 1)
연산자 표
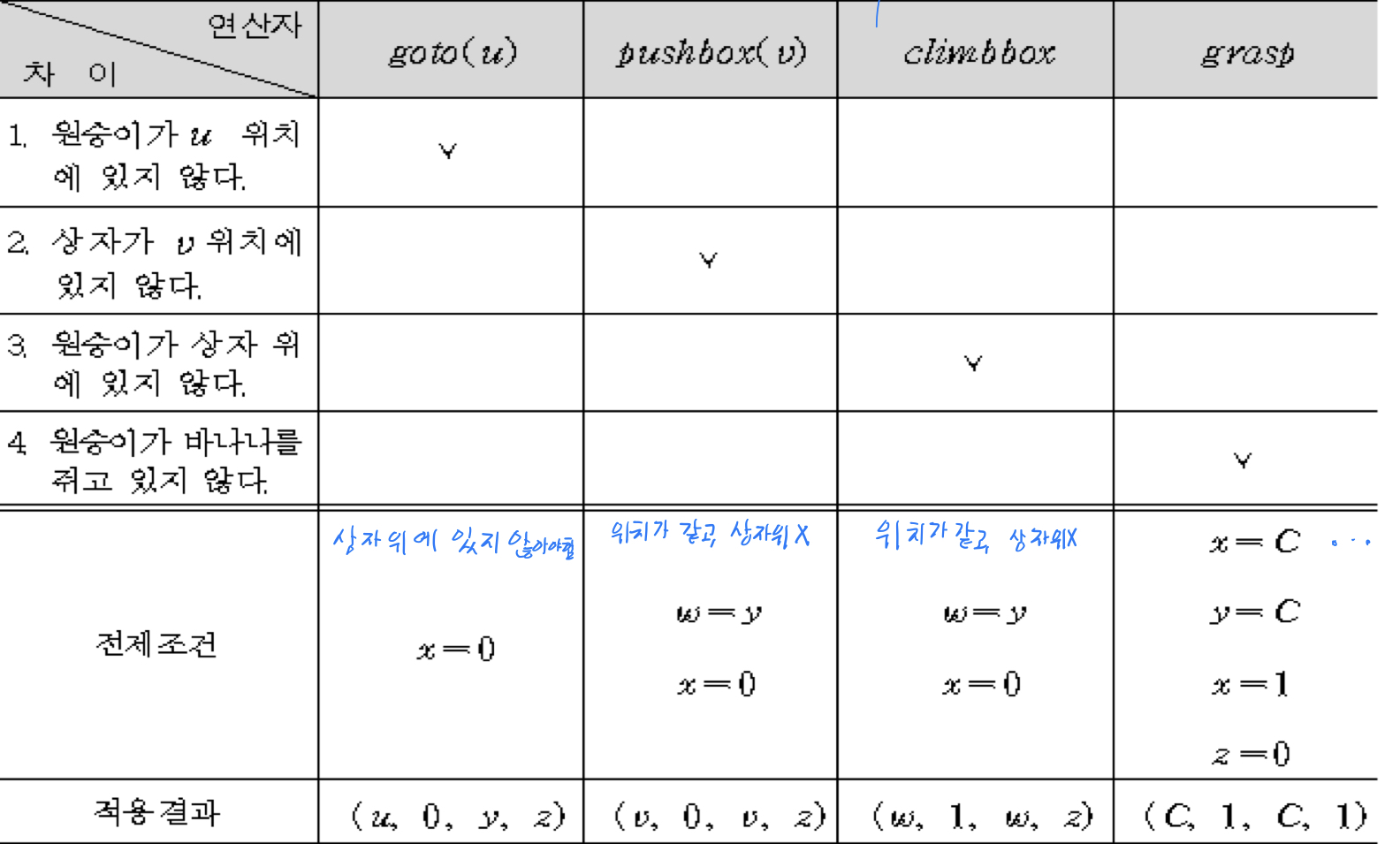
-
AND-OR Graph
-
개요
주어진 문제를 후계문제들의 조합으로 축소하는 과정을 표현하는 그래프
상태공간 탐색과 문제축소 기법 2가지가 있어야 문제를 AND-OR 그래프로 변환 가능
- 그래프의 탐색으로 얻을 수 있는 것
- 이 문제가 풀리는 문제인지 풀리지 않는 문제인지 판별
- 풀린다면 어떤 연산자 조합으로 풀 수 있는지 좋은 방법이 무엇인지 식별
- 풀이 그래프: 출발 노드가 풀이되었음을 보이는 풀이된 노드들로 구성된 부분 그래프
- 출발노드: 원래 문제 묘사
- 종단노드: 원시문제 묘사
- 풀이될 수 있는 노드에 대한 정의
- 종단 노드들은 원시문제에 해당되므로 풀이될 수 있다.
- 종단 노드가 아닌 노드로서 OR 후계노드들을 갖는 노드는 후계 노드 중 하나라도 풀이될 수 있다면 해당 노드 또한 풀이될 수 있다.
- 종단 노드가 아닌 노드로서 AND 후계노드를 갖고 있다면, 모든 후계노드가 풀이되어야 이 노드도 풀이된다.
- 풀이될 수 없는 노드에 대한 정의
- 종단이 아닌 노드로서 후계노드를 갖고 있지 않다면 풀이될 수 없는 노드이다.
- OR 후계노드를 갖고 있다면 후계노드들이 모두 풀이될 수 없다면, 풀이되지 않는다.
- AND 후계노드를 갖고 있다면 후계노드 중 하나라도 풀이되지 않는다면 풀이되지 않는다.
-
예시
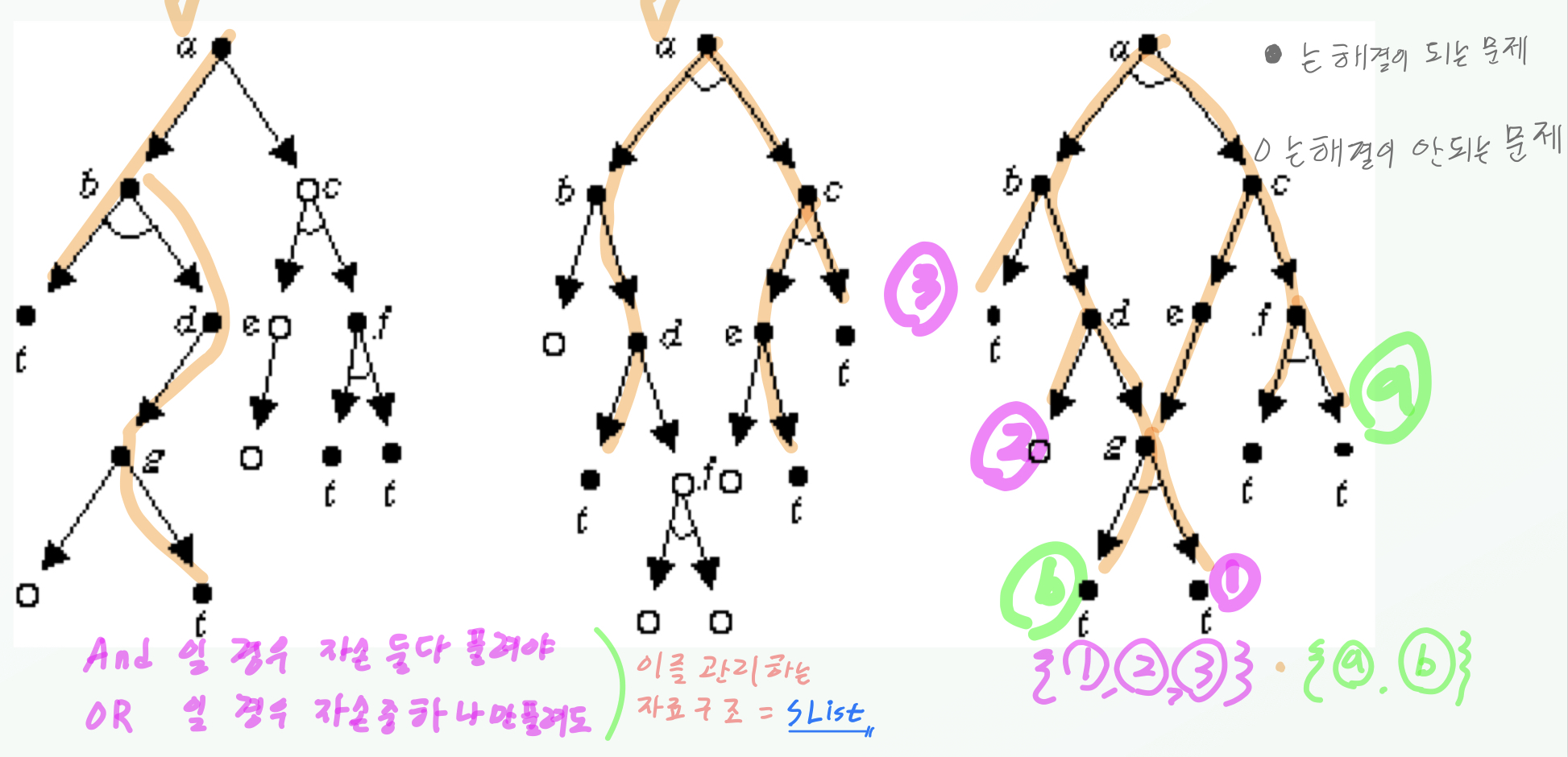
- 그래프의 탐색으로 얻을 수 있는 것
- 탐색 알고리즘 (넓이 우선 탐색)
- 출발노드를 OPEN 리스트에 넣는다. (OPEN은 선입선출로 운영됨)
-
출발노드가 풀이된 것 또는 풀이될 수 없다는 것이 밝혀질 때까지 다음을 반복한다.
2.1. OPEN으로부터 제일 앞에 있는 노드를 제거하여 이를 CLOSED에 넣는다. 이 노드를 n이라고 부른다.
2.2. n을 확장하여 모든 후계노드를 얻는다. 후계노드들을 OPEN의 끝에 넣고 포인터를 마련하여 n을 가리키게 한다. (여기서 OPEN의 앞에 넣으면 깊이 우선 탐색이 된다.)
2.3. 후계노드가 있는지 여부에 따라
2.3.1. 후계노드가 있다면
2.3.1.1. 후계 노드 중 종단 노드가 있다면
2.3.1.1.1. 탐색 트리에 풀이표시 프로시저를 적용한다.
2.3.1.1.2. 출발노드가 풀이된 것으로 표시되면 모든 탐색 종료
2.3.1.1.3. OPEN에서 풀이 되었거나 조상이 풀이된 노드들을 제거한다. (optional한 과정으로 한가지 이상의 풀이방법을 찾는데 낭비되는 시간을 줄이기 위함이다.)
2.3.2. 후계노드가 없다면
2.3.2.1. n을 풀이될 수 없는 것으로 표시한다.
2.3.2.2. 탐색트리에 풀이불가표시 프로시저를 적용한다.
2.3.2.3. 출발노드가 풀이될 수 없음으로 반별되면 모든 탐색을 종료한다.
2.3.2.4. OPEN에서 풀이될 수 없는 조상을 가진 노드들을 제거한다. (이건 필수적인 과정으로 이들은 전혀가능성이 없는 노드이기에 제거해야 옳다.)
- 풀이표시 알고리즘
- S-LIST라는 리스트에 풀이된 노드를 넣는다.
-
S-LIST에 더 이상 노드가 남아 있지 않거나 루트노드에 풀이표시가 될 때까지 다음을 반복한다.
2.1. S-LIST에서 하나의 노드를 꺼낸다. 이 노드를 n이라고 하자
2.2. 만일 노드 n이 그 노드의 부모노드(이하 p)의 AND 후계노드라면
2.2.1. 노드 n의 모든 형제노드에 풀이표시가 되어 있으면 노드 p에 풀이표시를 하고, S
-LIST에 넣는다.
2.3. 만일 n이 노드 p의 OR후계노드라면
2.3.1. 노드 p에 풀이표시를 하고, 노드 p를 S-LIST에 넣는다.
- 풀이불가표시 알고리즘
- S-LIST라는 리스트에 풀이 불가표시된 노드를 넣는다.
-
S-LIST에 더 이상 노드가 남아 있지 않거나 루트노드에 풀이불가 표시가 될 때까지 다음을 반복한다.
2.1. S-LIST에서 하나의 노드를 꺼낸다. 이 노드를 n이라고 하자
2.2. 만일 노드 n이 그 부모노드(이하 p)의 AND 후계노드라면
2.2.1. 노드 p에 풀이불가표시를 하고 노드 p를 S-LIST에 넣는다.
2.3. 만일 노드 n이 노드 p의 OR 후계노드라면
2.3.1. 노드 n의 모든 형제노드에 풀이불가표시가 되어 있으면, 노드 p에 풀이불가표시를 하고, 노드 p를 S-LIST에 넣는다.
10. 지식 표현
개요
- [데이터] -정리→ [정보] -개념화→ [지식] -보편화→ [진리]
- 위와 같은 계층 구조에서 데이터와 정보를 묶어 정보영역이라고 하며, 진리와 지식을 묶어 지식 영역이라고 한다.
- 지식: 합목적적의 개념화된 형태의 정보
- 지식과 문제의 해를 얻기 위해선 지식을 처리하는 메커니즘이 필요하다.
- 지식은 컴퓨터에서 처리가능해진 형태인 심볼의 형태로 묘사된다.
-
사실과 내부 표현 사이의 매핑
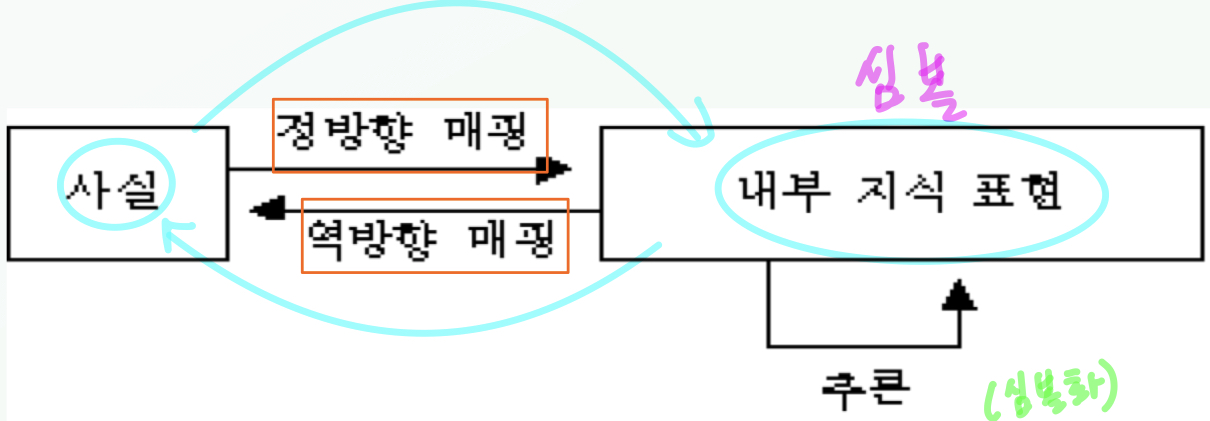
지식표현방법 4가지
- A. 논리를 이용한 지식표현
- 굉장히 정형화 되어 있으나 추론엔진이 돌아가는데 한계가 있음
- 논리를 이용한 추론은 명확하게 정의된 추론규칙을 이용하여 이미 참으로 알려진 사실로부터 새로운 사실을 유도한다.
- 논리의 예시
- 명제 논리
- 명제: 참 또는 거짓을 판단할 수 있는 문장
- 논리 연산자: 명제들을 연결해주는 매개
-
복합명제: 각 명제를 하나의 심볼로 표현하고 이 심볼들을 논리 연산자로 연결한 것
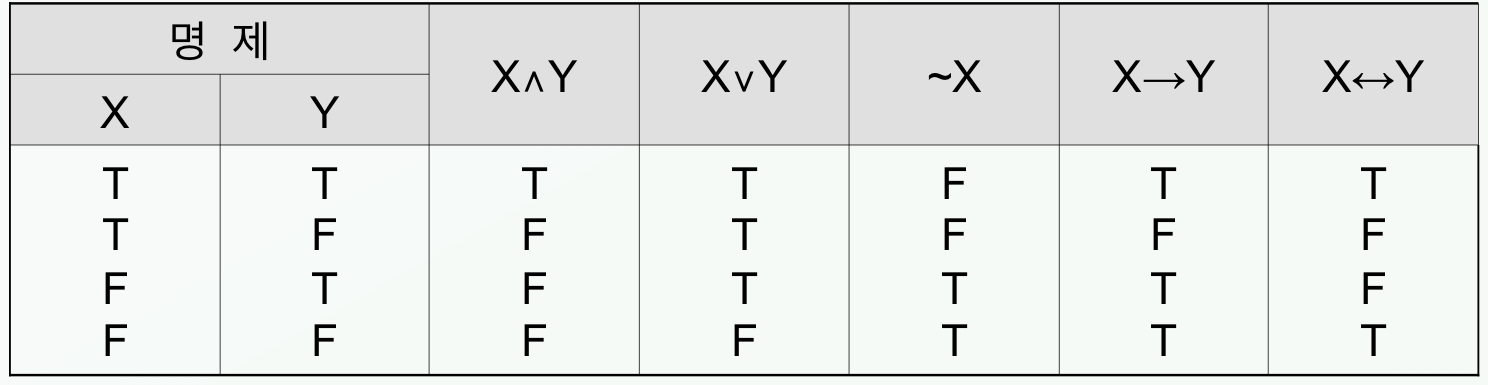
- Modus Pones(가언적 삼단논법): X, X → Y 라는 두 명제로부터 Y 명제를 도출하는 과정
- 술어논리
- 정형식: 술어, 상수, 변수, 한정자, 논리연산자 등 문법적으로 혀용된 방법으로 표현된 문장
- 술어와 객체로 표현 (객체에 변수 사용 가능)
- 고양이는 포유동물이다. → mammal (CAT)
- 장점: 객체 상호간 관계를 효율적으로 묘사
- 명제 논리
- B. 규칙을 이용한 지식표현
- 개요
- 규칙을 이용하여 표현된 지식 베이스
- 규칙은 조건(IF) -결론(THEN) 문장으로 표현
- 불이 났다 → 소방서에 연락한다.
- 액체의 ph가 6이하다 → 그 물질은 산이다.
- 장점
- 개개의 규칙은 독립적으로 추가, 삭제, 변경 가능
- 지식이 균일한 방법으로 표현되어 이해하기 쉬움
- 단점
- 대형 시스템에서 문제 풀이 과정의 제어흐름이 명확하지 않음
- 융통성이 적고 구조화되어 있지 않음
- 규칙을 이용한 추론 방법
- 전방향 추론 (forward chaining)
- 후방향 추론 (backward chaining)
- 추론사슬(inference chain): 여러개의 규칙을 적용할 시 순서가 있음
- 개요
- C. 시멘틱 네트를 이용한 지식표현
- 개요
- 지식 사이의 관계(순서)를 효율적으로 나타낼 수 있어 규칙기반 시스템의 단점 보완
- 노드의 집합과 이들 간의 아크로 구성
- 노드: 객체, 개념, 사건을 표현
- 아크: 노드사이의 관계를 표현
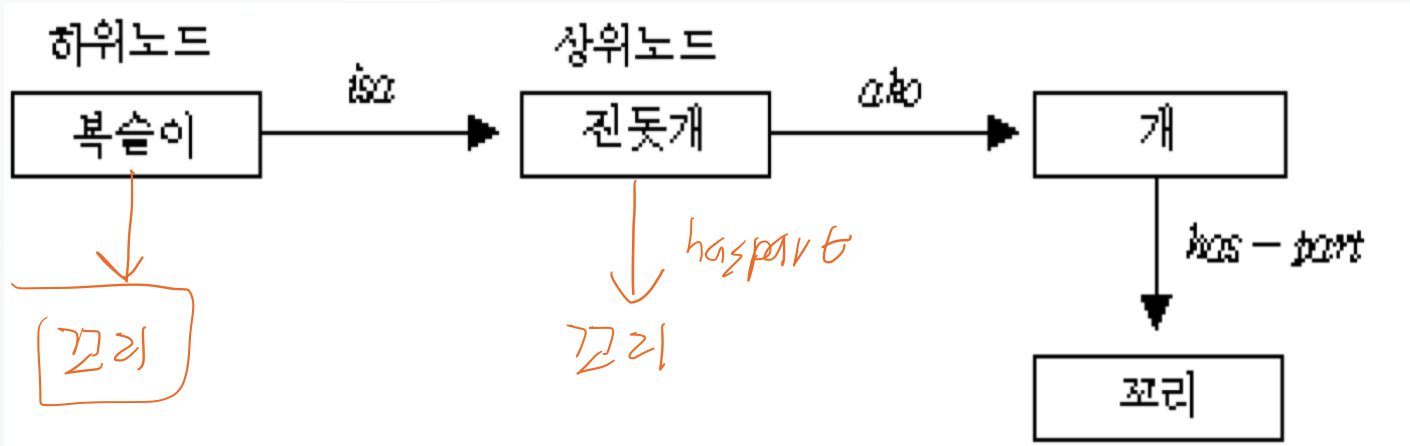
- isa(is a): 하나의 사례
- ako(a kind of): 어떠한 부류를 나타내는 개념의 한 종류 (상위 관계)
- has-part: 한 객체를 구성하는 구성품을 나타내는 관계
-
예제
사실 1) ako(진돗개, 개)
사실 2) isa(복슬이, 개)
사실 3) has-part(개, 꼬리)
-
- 장점
- 지식의 구성이 용이
- 지식의 수정 및 업데이트 용이
- 지식의 분배가 자동적으로 이루어짐
-
특성 상속에 의한 추론
하위 노드가 상위 노드의 속성을 따르는 것

- 개요
- D. 프레임을 이용한 지식표현
- 개요
- 지식을 서로 관계있는 것 끼리 분류하고 상하관계에 따라 구성한 것
- 객체지향 개념과 비슷
- 프레임 (frame)
-
슬롯(slot)과 그 슬롯에 저장된 값의 집합
슬롯은 프레임을 표현하는 하나의 속성(attribute)
객체지향 언어의 멤버에 해당.
-
한 프레임은 객체들의 집합을 표현
-
- 프레임의 특성상속(property inheritance)
- 부모 클래스로부터 슬롯과 값을 이어받는 것
- 부모클래스로부터 상속받는 것 이외에 자기자신의 고유한 슬롯을 가짐
- 프로시져(procedure)
- 멤버함수와 대응할 수 있음.
- 슬롯에는 그 슬롯의 사용과 관련된 프로시저가 연결
- 종류
- when-needed
- when-read
- when-written
- when-removed
-
예시

- 개요
11. 지식을 이용한 추론 A - Bayesian Inference
개요
- 확실히 경계가 그어진 그룹이 있을 때 어떤 지식의 소속 여부가 불확실 할 때 그것을 분류하는 추론
- 용어 정리
-
확률변수(probability variable)
하나의 사상에 대하여 하나의 값을 부여하는 함수
x라는 사건에 특정 수치를 부여하는 것 → f(x) = y
확률변수는 X, Y등 영어 대문자로 표현하며 그 값은 x, y와 같이 영어 소문자로 표현
-
표본공간 (sample space)
상호 배타적인 값들의 집합
변수 X의 표본공간은 $\Omega_X$로 표시
-
결합 확률 변수
Z = (X, Y): X와 Y의 곱집합 (conjunction)
Z의 표본공간: X와 Y의 표본공간의 곱, 즉 결합 표본공간 $\Omega_Z = \Omega_X \Omega_Y$
확률변수 집합 $\lbraceX_1, X_2, …, X_N\rbrace$에 대해 결합 표본공간은
$\Omega_{X_1}\times \Omega_{X_2} \times…\times \Omega_{X_n} = \prod_{i=1}^N \Omega_{X_i}$
-
샘플 집합$X = \lbracex_1, x_2,…, x_N\rbrace$에서 평균
$\mu = \frac {1}{N}\Sigma_{i=1}^{N}x_i$
-
샘플 집합에서 분산
$\Sigma = \frac{1}{N-1}\Sigma_{i = 1}^{N}(x_i - \mu)(x_i - \mu)^T$
-
X, Y의 공분산
$\Sigma = \frac{1}{n}\Sigma_{k = 1}^{N}(x_k - \mu_x)(y_k - \mu_y)^T$
-
베이즈정리
| $P(w_i | \mathbf{x}) = \frac{P(\mathbf{x} | w_i)P(w_i)}{P(\mathbf{x})} = \frac{우도 * 사전확률}{P(\mathbf{x})}$ |
-
사후확률 P($w_i$ $\mathbf{x}$) $X$ 가 주어졌을 때 그것이 부류 $w_i$에서 발생했을 확률 (사후확률)
-
사전확률 P($w_i$)
사건 발생 이전의 확률 즉, 선택 이전 기반사건의 확률
-
우도함수 P($\mathbf{x}$ $w_i$) $w_i$ 그룹에 $\mathbf{x}$ 가 속해있을 확률
베이지안 분류기
- 개요
- 분류기 학습(훈련)에 사용하는 정보는 ‘훈련집합’
- 훈련집합 $X = \lbrace(\mathbf{x}_1, t_1), (\mathbf{x}_2, t_2), …, (\mathbf{x}_N, t_N)\rbrace$
- $\mathbf{x} = (x_1, x_2, …, x_d)$는 특징 벡터 (관측 벡터)
- $t_i\in\lbracew_1, w_2, …, w_M\rbrace$ 부류 표지 (true class, 정답)
- 훈련집합 $X = \lbrace(\mathbf{x}_1, t_1), (\mathbf{x}_2, t_2), …, (\mathbf{x}_N, t_N)\rbrace$
- 분류기 학습(훈련)에 사용하는 정보는 ‘훈련집합’
- 최소 오류 베이지안 분류기
- 개요
- 주어진 특징 벡터 $\mathbf{x}$에 대해 ‘가장 그럴듯한’ 부류로 분류
- 분류 결과의 채점은 맞다 또는 틀리다 로 구성되어 얼마나 틀린지 는 평가되지 않음
-
사후확률, $P(w_i \mathbf{x})$ 를 이용 -
$P(w_1 \mathbf{x}) >P(w_2 \mathbf{x})이면, \mathbf{x}를 w_1으로 분류하고$ -
$P(w_1 \mathbf{x}) <P(w_2 \mathbf{x})이면, \mathbf{x}를 w_2으로 분류하라$
-
- But! 일반적으로 사후확률은 직접 구할 수 없기 때문에 베이즈 정리를 이용해 사후확률 계산을 사전확률과 우도로 대체
- 참고
-
$P(w_i \mathbf{x}) = \frac{P(\mathbf{x} w_i)P(w_i)}{P(\mathbf{x})} = \frac{우도 * 사전확률}{P(\mathbf{x})}$ -
여기서 분모인 $P(\mathbf{x})$는 모든 경쟁자 가능성 $P(w_i \mathbf{x})$들이 공통적으로 갖기 때문에 각 $P(\mathbf{x})$이 비슷하다면 생략 가능하다. - 사전확률 계산
- $P(w_1)=n_1/N, P(w_2)=n_2/N$
- 정확한 값이 아니라 추정이며 N이 커질수록 실제 값에 가까워진다.
- 우도 계산
-
훈련 집합에서 $w_i$에 속하는 샘플들을 가지고 $P(\mathbf{x} w_i)$추정 - 분류기의 핵심이 되는 과정이다!
-
-
- 분류 결과의 오류 확률
-
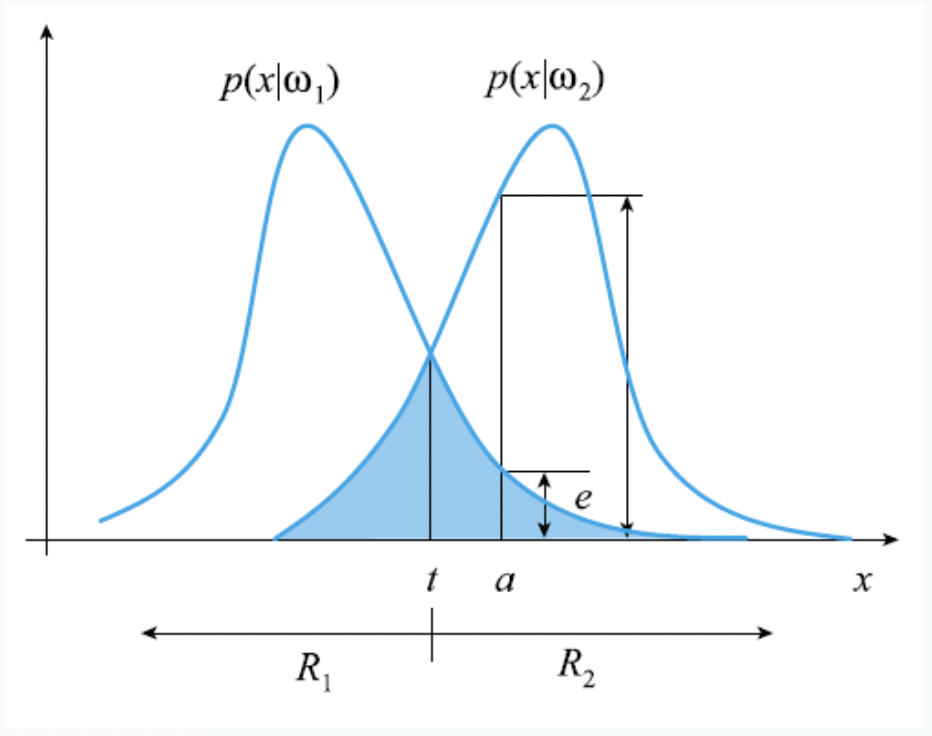
부류가 $w_1,\ w_2$ 일 경우
-
분류 결과의 오류 확률
$E=\frac{1}{2}\left( {\int_{-\infty}^{t} P(x w_2)\, dx + \int^{\infty}_{t} P(x w_1)\, dx}\right)$ -
도해의 t 는 thrashold 로 분류의 기준이 되는 경계값이라고 할 수 있다.
- t를 기준으로 왼쪽은 $w_1$로, 오른쪽은 $w_2$로 분류한다.
- 여기서 파란색으로 색칠된 부분은 오분류 가능성이 상당한 구간을 뜻한다.
-
-
M 부류 최소오류 베이지안 분류기
-
사전확률과 우도로 나타낼 경우
$\max p(\mathbf{x} w_i)P(w_i)\ 이\ 되게\ 하는\ i\ 값이\ k 일때\ w_k로\ 분류한다.$
-
-
- 개요
- 최소 위험(손실) 베이지안 분류기
- 개요
- 성능을 평가하는 척도로 이진분류인 오류가 적절하지 않은 상황에서 사용
-
정상인과 암환자의 분류시
암환자를 정상인으로 분류시 손실 > 정상인을 암환자로 분류시 손실
-
-
손실 행렬을 사용하여 틀릴 경우 손실에 대해 측정
손실행렬 $C = \begin{pmatrix} c_{11} & c_{12} \ c_{21} & c_{22} \end{pmatrix}$
$c_{11}: w_1에\ 해당하는\ 것을\ 옳게\ 분류한\ 경우의 \ 손실$
$c_{12}: w_2에\ 해당하는\ 것을\ w_1로\ 오분류한\ 경우의\ 손실$
- 성능을 평가하는 척도로 이진분류인 오류가 적절하지 않은 상황에서 사용
- 분류기준
-
부류가 $w_1,\ w_2$ 일 경우
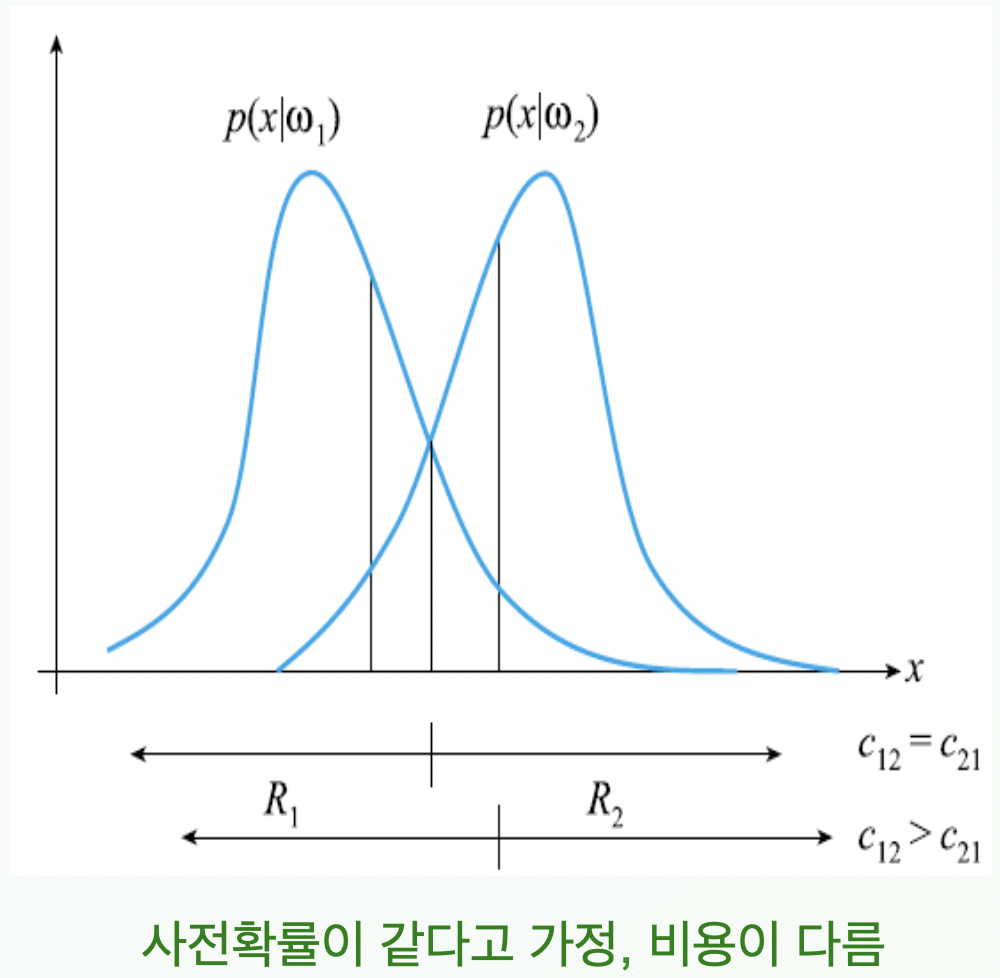
- $\mathbf{x}를 q_2 > q_1이면 w_1로 분류하고, q_2 < q_1이면 w_2로 분류$
-
$q_1=c_{11}p(\mathbf{x} w_1)P(w_1)+c_{21}p(\mathbf{x} w_2)P(w_2)$ -
$q_2=c_{12}p(\mathbf{x} w_1)P(w_1)+c_{22}p(\mathbf{x} w_2)P(w_2)$ $q_1:\ w_1으로\ 분류시\ 손실,\ q_2:\ w_2으로\ 분류시\ 손실$
-
-
우도비 결정 규칙을 유도할 수 있다.
$T\ =\ \frac{(c_{21} - c_{22})P(w_2)}{(c_{12} - c_{11})P(w_1)}\ 이라고\ 할\ 때$
$\frac{p(\mathbf{x} w_1)}{p(\mathbf{x} w_2)} > T\ 이면\ w_1로\ 분류하고,\ \frac{p(\mathbf{x} w_1)}{p(\mathbf{x} w_2)} < T\ 이면\ w_2로\ 분류하라$ 이때 $T$ 는 분류 기준인 경계값이 된다!
- $\mathbf{x}를 q_2 > q_1이면 w_1로 분류하고, q_2 < q_1이면 w_2로 분류$
-
M 부류의 최소 오류 베이지안 분류기
- $\mathbf{x}를\ k=\arg\min q_i일\ 때 w_k로\ 분류하라.$
-
$이때\ q_i=\Sigma_{j=1}^{M}\lbracec_{ji}p(\mathbf{x} w_j)P(w_j)\rbrace$
-
- 개요
- 식별 함수로 M부류 베이지안 분류기 간소화
- 준비
-
$f(.)$가 단조 증가(구간 내에서 증가만 하는 함수)라면 $p(\mathbf{x} w_i)P(w_i)$ 대신 $g_i(\mathbf{x})=f(p(\mathbf{x} w_i)P(w_i))$를 사용하여 비교하여도 결과는 같다. - 이때 $f(.)$로 주로 $\log$ 함수를 사용한다.
-
정규분포의 수식표현
$N(\mu, \sigma^2)=\frac{1}{(2\pi)^{1/2}\sigma}\exp \left({-\frac{(x-\mu)^2}{2\sigma^2}}\right)$
2차원 공분산을 이용한 정규분포
$N(\mu, \Sigma)=\frac{1}{(2\pi)^{\frac d2} \Sigma ^{\frac12}}\exp ({-\frac{1}{2}(\mathbf{x}-\mu)^T}\Sigma^{-1}(\mathbf{x}-\mu))$
-
- 우도가 정규분포를 따른다는 가정 하에 베이지안 분류기를 간소화 하면
-
우도
$p(\mathbf{x} w_i)=N(\boldsymbol{\mu}_i,\boldsymbol{\Sigma}_i)=\frac{1}{(2\pi)^{\frac d2} \boldsymbol{\Sigma}_i ^{\frac12}}\exp ({-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu}_i)^T}\boldsymbol{\Sigma}_i^{-1}(\mathbf{x}-\boldsymbol{\mu}_i))$ -
우도함수에 로그를 취해 간소화 하면
$g_i(\mathbf{x})= \ln (\ p(\mathbf{x} w_i)\ P(w_i)\ )$ $g_i(\mathbf{x})=\ln N(\boldsymbol{\mu}_i,\boldsymbol{\Sigma}_i) + \ln P(w_i)$
$g_i(\mathbf{x})= {-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu}_i)^T}\boldsymbol{\Sigma}_i^{-1}(\mathbf{x}-\boldsymbol{\mu}_i) - \frac{d}{2}\ln2\pi-\frac12\ln \boldsymbol{\Sigma}_i +\ln P(w_i)$
-
- 준비
-
식별함수를 이용한 M부류 결정 경계
$g_{ij}(\mathbf{x})=g_i(\mathbf{x})-g_j(\mathbf{x}) = 0\ 인\ 점들의\ 집합$
- 나이브 베이지안 가정하
- 나이브 베이지안이란?
- 모든 부류가 서로 독립이고(Independent)
- 모든 부류가 같은 공분산을 공유하고(Identically distributed)
- 모든 부류가 앞의 (i.i.d)가정을 반영한 가우시안 분포를 따른다고 가정.
장점: 차원의 저주(연산량 폭증)을 피함
단점: 성능(분류 정확도) 저하
$g_{ij}(\mathbf{x})=\left({(\boldsymbol{\Sigma}^{-1}(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j)}\right)^T\left({\mathbf{x}-\left({\frac12(\boldsymbol{\mu}_i+\boldsymbol{\mu}_j)-\frac{\boldsymbol{\mu}_i-\boldsymbol{\mu}_j}{(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j)^T\boldsymbol{\Sigma}^{-1}(\boldsymbol{\mu}_i-\boldsymbol{\mu}_j)}\ln\frac{P(w_i)}{P(w_j)}}\right)}\right)$
- 나이브 베이지안이란?
-
비선형 분류 (NOT naive)
$g_{ij}(\mathbf{x})=g_i(\mathbf{x})-g_j(\mathbf{x}) = 0\ 를\ 각각의 \boldsymbol{\Sigma}_i,\ \boldsymbol{\Sigma}_j\ 를\ 이용해\ 연산해야\ 한다.$
- 나이브 베이지안 가정하
특성
- 확률분포 모델링의 정확도에 따라 분류 정확도가 좌우된다.
- 실제 데이터와 일치하는 확률분포 값$(\boldsymbol{\mu,\ \Sigma})$을 알 경우 최적의 분류 성능 보장
- 실제로 그것은 불가능하기에 근사치를 이용한 분류가 이루어져 비현실성을 내포
12. 지식을 이용한 추론 B - Fuzzy Inference
개요
-
퍼지집합이란?
소속 여부가 확실하지 않은 경우의 집합 - 수학적 집합과 배치(背馳)
Ex) 키 큰 사람의 집합, 맛있는 커피의 집합
-
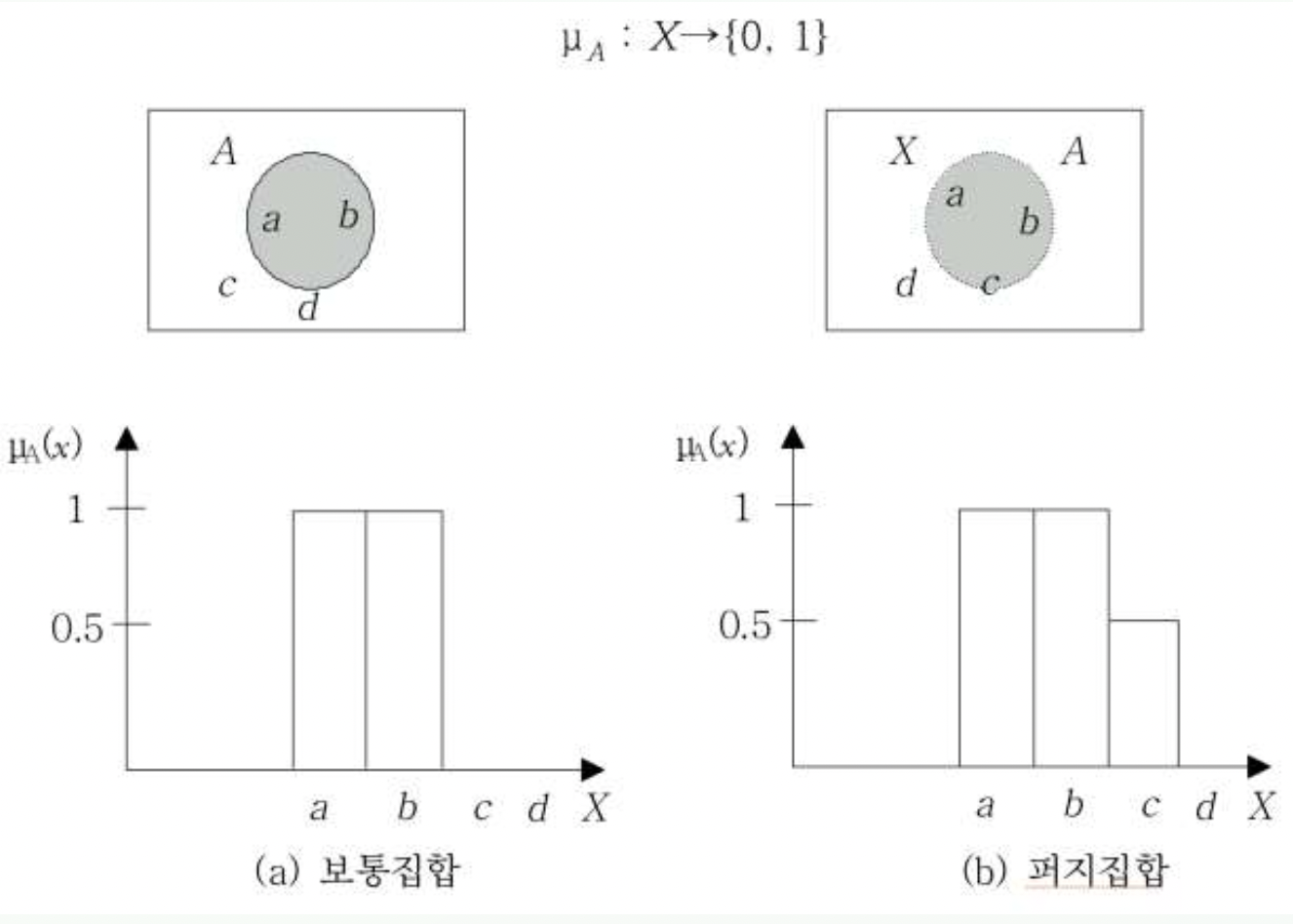
소속 함수(membership function)
$\mathbf{x}$가 집합 $A$에 소속될 확률 = $\mu_A(\mathbf{x})$
소속함수는 전체집합 $X$ 의 모든 원소를 집합 $\lbrace0,\ 1\rbrace$에 mapping
-
집합 연산 기초
-
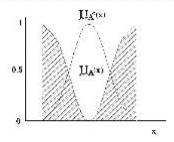
여집합
$\mu_{\bar{A}}(\mathbf{x})=1\ -\ \mu_A(\mathbf{x}),\ \ \forall\mathbf{x}\in X$
-
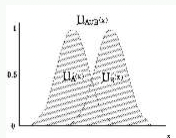
합집합
A또는 B에 소속될 확률 :
$\mu_{A\cup B}(\mathbf{x})=\max[\mu_A(\mathbf{x}),\ \mu_B(\mathbf{x})],\ \ \forall\mathbf{x}\in X$
-
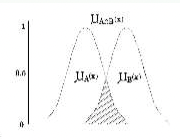
교집합
A와 B모두에 소속될 확률:
$\mu_{A\cap B}(\mathbf{x})=\min[\mu_A(\mathbf{x}),\ \mu_B(\mathbf{x})],\ \ \forall\mathbf{x}\in X$
-
상등
정의: $A = B\ \ \mathrm{if}\ \ \mu_A(x) = \mu_B(x)\ \mathrm{for}\ \forall x\in X$
Ex) 퍼지집합
$A=\lbrace(1,\ 1),(2,\ 0.5),(3,\ 0)\rbrace$
$ B= \lbrace \mathrm{y}|\mathrm{y}=-0.5\mathrm{x}+1.5,\mathrm{for}\ \mathrm{x}=1,2,3 \rbrace $ $ $
$A=B$
-
포함
정의: $A\subset B\ \mathrm{if}\ \mu_A(x) < \mu_B(x)\ \mathrm{for}\ \forall x\in X$
Ex) 퍼지집합
$A=\lbrace키\ 큰\ 사람\rbrace,\ \ B=\lbrace키가\ 작지\ 않은\ 사람\rbrace$
-
퍼지 관계
-
집합 $X,\ Y$사이의 퍼지 관계 $R$의 소속함수
$\mu_R:X\times Y \rightarrow\ [0,\ 1]$
0 이상 1 이하의 어떤 값
$X = \lbracex_1,\ x_2,…,\ x_n\rbrace,\ Y=\lbracey_1,\ y_2,…,\ y_m\rbrace\ 일\ 때,$
$R=\begin{bmatrix}\mu_R(x_1,\ y_1),\ & \cdots & \mu_R(x_1,\ y_m)
\vdots & \ddots & \vdots
\mu_R(x_n,\ y_1),\ & \cdots & \mu_R(x_n,\ y_m) \end{bmatrix}$ -
퍼지 역관계
$\mu_R^{-1}(y, x)=\mu_R(x, y)\ \ \mathrm{for}\ \ (y, x)\in Y \times X$
-
퍼지 합집합 관계
$\mu_{P\cup R}(x, y) = \max\lbrace\mu_P(x, y),\ \mu_R(x, y)\rbrace\ \ \mathrm{for}\ \ \boldsymbol\forall(x, y)\in X\times Y$
각 엘리먼트 별로 Max 값을 취하면 된다.
-
퍼지 교집합 관계
$\mu_{P\cap R}(x, y) = \min\lbrace\mu_P(x, y),\ \mu_R(x, y)\rbrace\ \ \mathrm{for}\ \ \boldsymbol\forall(x, y)\in X\times Y$
각 엘리먼트 별로 Min 값을 취하면 된다.
-
퍼지 역집합 관계
$\mu_{R^c}(x, y) = 1-\mu_{R}(x, y)\ \ \mathrm{for}\ \ \boldsymbol{\forall}(x,y)\in X \times Y$
-
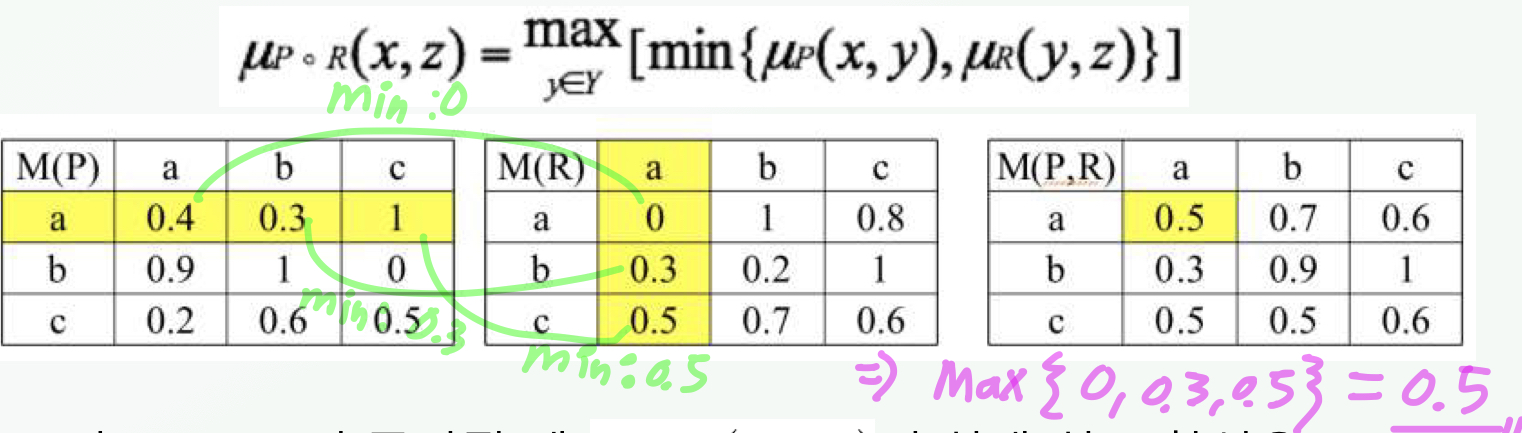
퍼지 관계의 합성
추론 교칙의 합성법: 대응하는 각 셀의 최소값을 구한 후 이들의 최대값을 선택
퍼지 논리
-
퍼지 논리식 f
논리식의 값이 구간 $[0, 1]$사이의 값을 가질 수 있도록 확장
$\mathrm f :[0,1]^n \rightarrow [0,1]$
- 퍼지 논리식의 연산자
-
부정 (negation)
$\bar{\mathrm{a}} = 1 - \mathrm{a}$
-
논리곱 (conjunction)
$\mathrm{a}\land\mathrm{b} = \min(\mathrm{a},\mathrm{b})$
-
논리합 (disjunction)
$\mathrm{a}\lor\mathrm{b} = \max(\mathrm{a},\mathrm{b})$
-
조건명제 (implication)
$\mathrm{a}\Rightarrow\mathrm{b} = \min(1,\ 1-\mathrm{a}+\mathrm{b})$
-
-
퍼지 술어
술어에서 객체의 성질을 나타내는 술어가 퍼지집합일 때 퍼지술어(fuzzy prediction)으로 정의됨
퍼지 이론 응용 분야
- 인공지능, 지능 제어, 전문가 시스템, 패턴 인식
- 의료, 정보 검색, 가전제품
- 의사 결정 지원, 앙케이트 조사
Human annotation
-
Human annotation을 사용 할 때 학습의 기준이 되는 진리표가 필요하다.
이 진리표는 복수의 사람이 실제 데이터를 분석한 것을 이용하여 만들어진다.
- 이러한 진리표를 만드는데 몇 가지 장애 요인이 있다.
-
사람의 감정의 스펙트럼이 넓고, 같은 자극에도 개인간 편차가 존재한다.
→ variance between persons
-
더욱이 같은 사람이라도 당시의 컨디션 등 통제할 수 없는 외부 요인에 의해 판정이 달라질 수 있다.
→ variance within a person
-
-
예시

13. Learning and NNs
학습
-
학습이란?
학습이란 기억으로부터 기술이나 지식, 이해, 가치, 지혜를 습득, 발전 시키는 과정으로 경험의 산물이자 교육의 목표라고 할 수 있다.
-
기계적 학습
새로운 지식을 저장을 통해 이후의 똑같은 상황에서는 먼저 행한 계산을 반복하지 않고도 단순히 저장된 결과를 검색하여 사용하는 것
- 기계학습의 메커니즘
-
문제와 해를 기억하는 방법을 사용
$[(X_1,…)]$ -<풀이함수>→ $[(Y_1,...)]$ -<저장>→ $[(X_1,...X_n), (Y_1,...Y_n)]$
- 정보의 체계적 저장
- 일반화
- 초점의 방향
-
- 기계학습의 메커니즘
- 개념 학습(Concept Learning)
-
유형화
입력을 분류하여 그가 속한 한 유형의 이름을 주는 과정
- 함수 이용 방법: 작업 영역에 관련된 일련의 특성들을 색출 후, 점수 함수에 의해 유형을 정의 (regression(회귀) 기법)
- 구조적 방법: 특성들 간의 구조(primitive)로 정의
-
예시

-
-
- 예제에 의한 학습
- 개요
- 개념학습과 대비된다. ← 어떤 함수의 형태로 분류됨
- 입력을 주면 결과가 나오는 end to end 학습.
- 특수한 예들을 입력하여 행동부분의 성능을 향상시켜서 일반적인 규칙을 도출하는 것
- 예제가 들어올수록 규칙이 정확해진다.
- 학습부분과 행동부분으로 구성
- 인공 신경망이 대표적이다.
- 개요
Neural Networks (신경망)
- 개요
-
인공 신경망(Artificial Neural Network: ANN)
뇌의 정보처리를 모방하여 인간에 필적하는 지능을 가진 컴퓨터
- 인간의 신경 세포인 시넵스에 대응하는 Perceptron을 단위로 구현
- Perceptron: 1958년 Rosenblatt이 제안, 학습 가능함을 증명
- 인간 두뇌의 연산은 패턴/연상기반 이라면, 컴퓨턴느 논리/산술적 연산 기반이다.
- 인간의 신경 세포인 시넵스에 대응하는 Perceptron을 단위로 구현
-
- 퍼셉트론 (Perceptron)
- 개요
- 생물학적 신경세포의 작동원리를 수학적으로 모델링한 인공 뉴런
- 뇌의 구조를 모사한 정보처리 방식
-
개념도
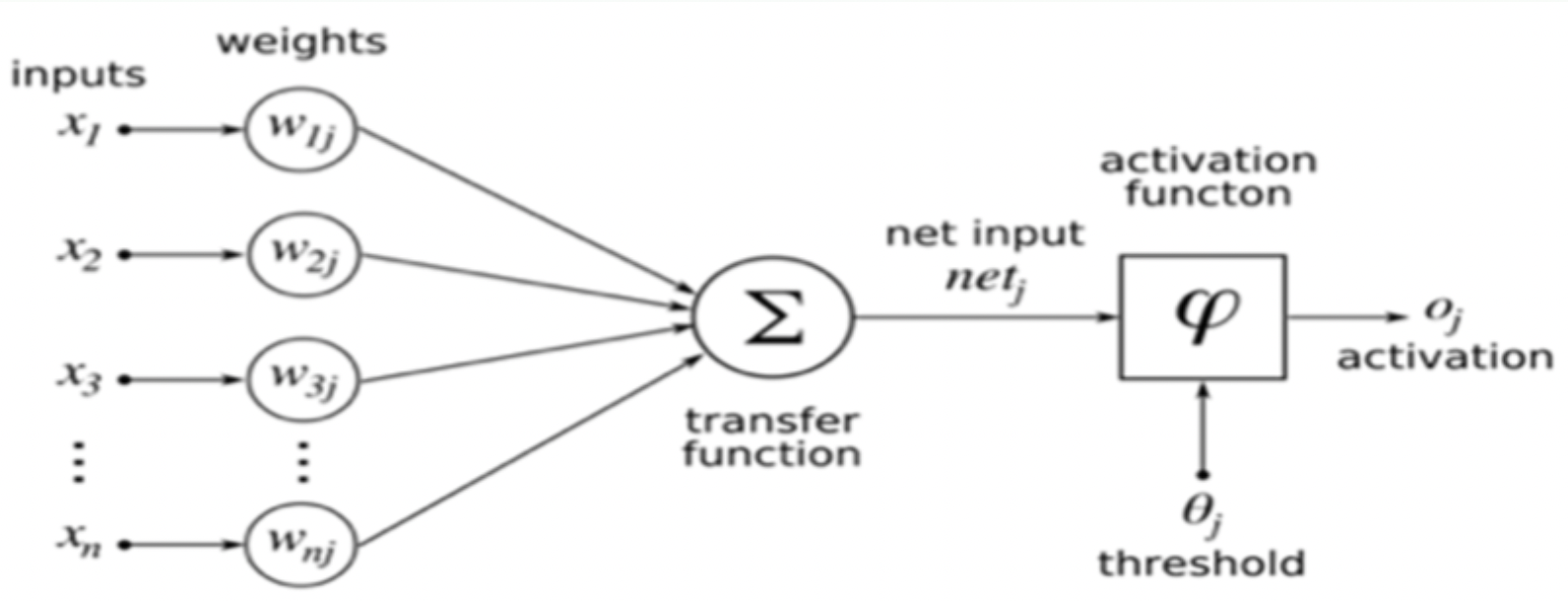
- 입력: $x_1,\ x_2,…,\ x_n$으로 이루어진 벡터 $X$
- 가중치: $w_1,\ w_2,…,\ w_n$로 이루어진 벡터 $W$
- $o_j=(X^T * W_j > \theta_j)?\ 1:0$
- 구조와 원리
-
입력층: d+1개의 노드 (특징 벡터 X)
d+1 인 이유: threshold 값을 별도로 저장하지 않고 입력층으로 받도록 한 것.
(해당 입력은 항상 흥분)
threshold 따로 보관한다면 d개 입력을 받는다.
- 출력층: 한개의 노드의 이진 출력($\therefore$ 2부류 분류기가 된다.)
-
Edge 와 가중치
구조 도식화
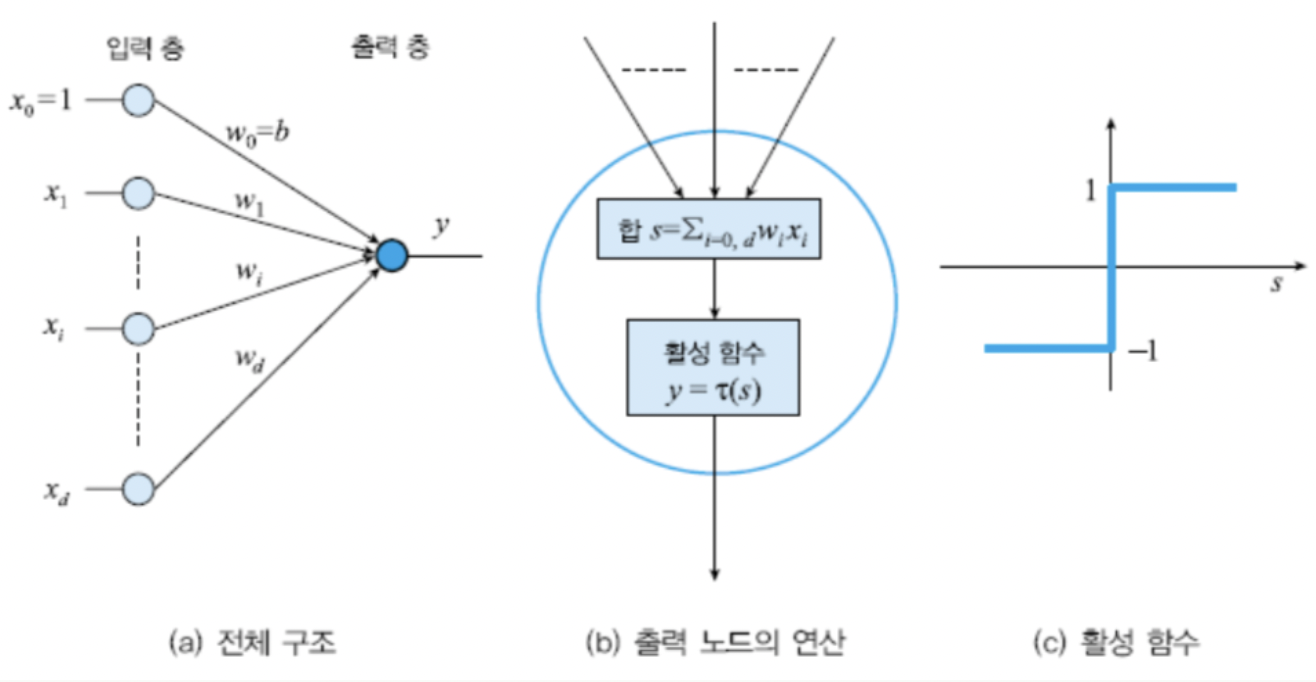
-
노드의 연산
$y = \tau(s) =\tau\left({\Sigma_{i=1}^dw_ix_i+b}\right) = \tau(\mathbf{w}^T\mathbf{x} + b)$
$이때 \tau(s)=\begin{cases}+1,& s \ge 0
-1,&s<0\end{cases}$$w_i = 가중치,\ x_i=흥분여부,\ b=\mathrm{bias}$
-
퍼셉트론은 선형 분류기이다.
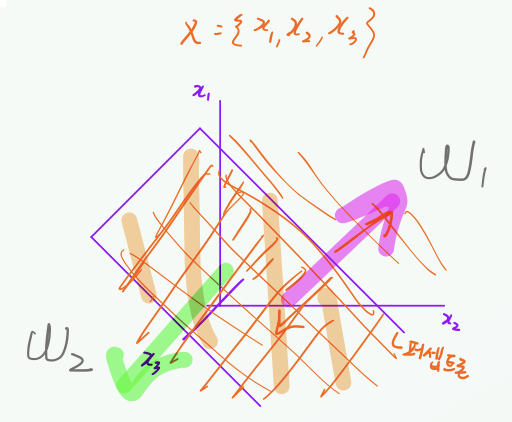
-
- 활성화 함수
-
Step function
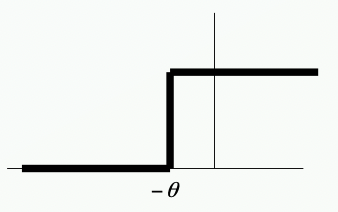
$O = \begin{cases}1&\Sigma_{i=0}^nw_i\mathrm{I}+\theta>0 \ 0 & \mathrm{otherwise}\end{cases}$
-
Sigmoid function
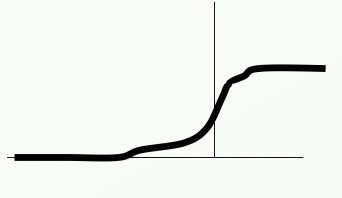
$O = \frac{1}{1+e^{-\Sigma_{i=0}^nw_i\mathrm{I}+\theta>0}}$
- 완만하게 변화
- 미분 가능하다
-
- 개요
- 퍼셉트론 학습
- 개요
-
훈련 집합 $X=\lbrace(\mathbf{x}_1,\ t_1),\ (\mathbf{x}_2,\ t_2),…,(\mathbf{x}_N,\ t_N)\rbrace$이 주어졌을 때 이들을 모두 옳게 분류하는 퍼셉트론 $(\mathbf{w},\ b)$를 찾는 것을 말한다.
이때, 샘플의 $\mathbf{x}_i$는 특징 벡터, $t_i$는 부류 표지를 의미한다. 예를 들어$\mathbf{x}_i \in w_1$ 이면 $t_i=1$이 된다.
-
-
패턴 인식에서 학습 알고리즘 설계과정
단계 1: 분류기 구조 정의와 분류 과정의 수학식 정의
단계 2: 분류기 품질 측정용 비용함수 $\mathrm{J}(\Theta)$정의 $(\ 매개변수\ 집합\ \Theta = \lbrace\mathbf{w}^T, b\rbrace\ )$
단계 3: $\mathrm{J}(\Theta)$를 최적화 하는 $\Theta$를 찾는 알고리즘 설계
- 예시
- 단계 1 분류기 식: $y = \tau(s) =\tau\left({\Sigma_{i=1}^dw_ix_i+b}\right) = \tau(\mathbf{w}^T\mathbf{x} + b)$ 매개변수 집합: $\Theta = \lbrace\mathbf{w}^T, b\rbrace$
- 단계 2
$\mathrm{J}(\Theta)=\Sigma_{\mathbf{x}_k\in Y}(-t_k)(\mathbf{w}^T\mathbf{x}_k+b)$
- $Y$: 오분류된 샘플 집합
- $\mathrm{J}(\Theta)$는 항상 양수
- $|Y|$가 클수록 $\mathrm{J}(\Theta)$의 값도 증가 $ $ (즉, 이 둘이 클수록 안좋은 $\Theta$)
-
단계 3
$\mathrm{J}(\Theta)=0\ 인\ \Theta$ 를 찾는 것이 목표
-
내리막 경사법 이용
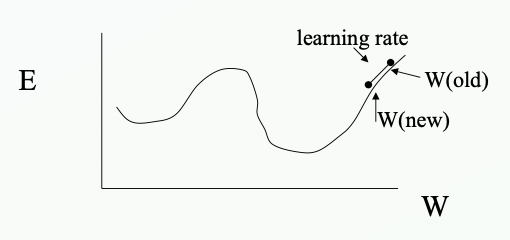
- 현재 해 $\Theta$를 $\frac{-\sigma}{\sigma\Theta}$방향으로 이동
- 이때 학습률 $\rho$를 곱하여 조금씩 이동
- local optima에 빠지지 않는다. unimodal이기 때문
-
- 예시
- Delta rule
- 내리막 경사법의 학습
$\Theta(h+1) = \Theta(h)-\rho(h)\frac{\theta\mathrm{J}(\Theta)}{\theta\Theta}$
\[\begin{cases}\mathrm{bias}를\ \mathbf{w}와\ 구분한\ 경우&\left.{\begin{matrix}\mathbf{w}(h+1) &=&\mathbf{w}(h)+\rho(h)\Sigma_{\mathbf{x}_k\in Y}t_k\mathbf{x}_k \\ b(h+1)&=&b(h)+\rho(h)\Sigma_{\mathbf{x}_k\in Y}t_k\end{matrix}} \right\rbrace \\ \\ \mathrm{bias}를\ \mathbf{w}에\ 포함시켰다면&\hat{\mathbf{w}}(h+1)= \hat{\mathbf{w}}(h)+\rho(h)\Sigma_{\mathbf{x}_k\in Y}t_k\mathbf{x}_k\end{cases}\] - 학습 방법 A -batch mode
- 배치 단위로 학습
- 분류 함수 $y = \tau(\mathbf{w}^T\mathbf{x}_i+b)$
- 배치에서 오분류된 셈플 집합 $Y$를 수집
- $\Theta$ 업데이트 또한 배치 단위로 이루어짐
- 같은 배치 반복학습
- 학습 종료 조건 $Y = \empty$
- 학습 방법 B -pattern mode
- 여러개의 패턴$(\mathbf{x}_1,\ t_1)\ 쌍$이 담긴 훈련 집합 $X$를 이용해 학습
- 분류 함수 $y = \tau(\mathbf{w}^T\mathbf{x}_i+b)$
- 패턴 하나를 입력할 때 마다 만약 오분류 되었다면 가중치를 업데이트한다.
- $X$집합의 패턴들을 반복하여 학습
- 학습 종료 조건: $X$ 의 모든 패턴을 입력 했을 때 모든 $i$에 대해 $y == t_i$ 가 참일 때
- 개요
- 다층 퍼셉트론 MLP
- 개요
- 퍼셉트론의 한계
-
선형 분리가 불가능한 상황(선형 분류시 오분류되는 $\mathbf{x}$가 항상 존재하는 상황)에 대응 불가
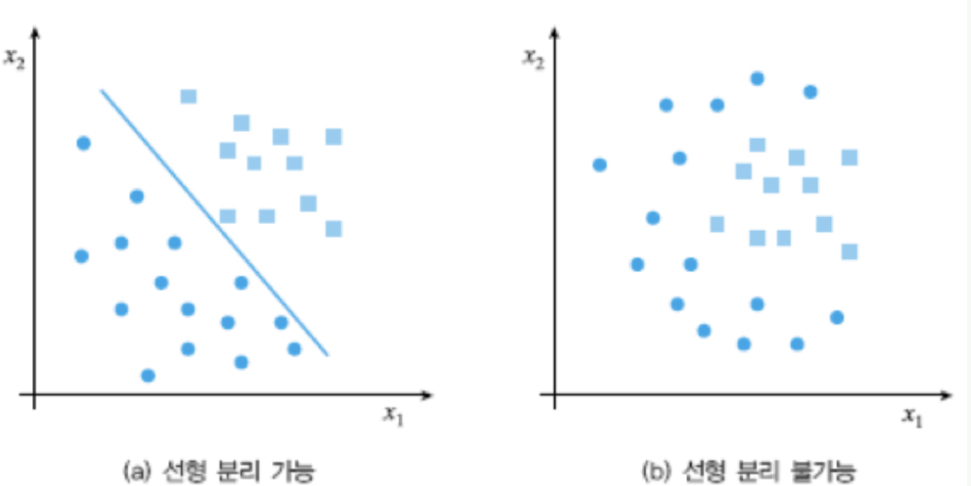
-
XOR 문제
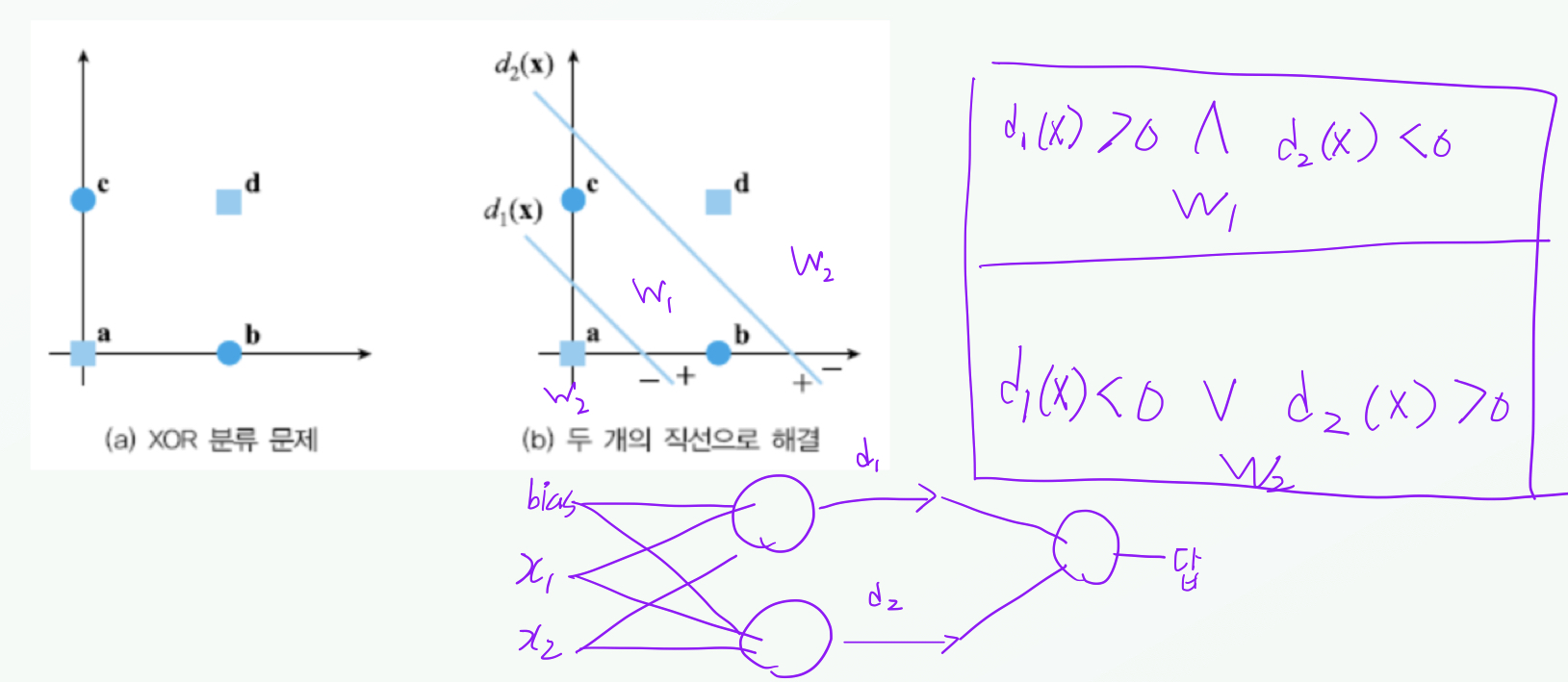
-
- 퍼셉트론의 한계
- 다층 퍼셉트론의 아키텍처
- 입력측, 은닉층, 출력층
- 각 층간 엣지의 가중치 집합들
-
그림을 보며 이해해보자
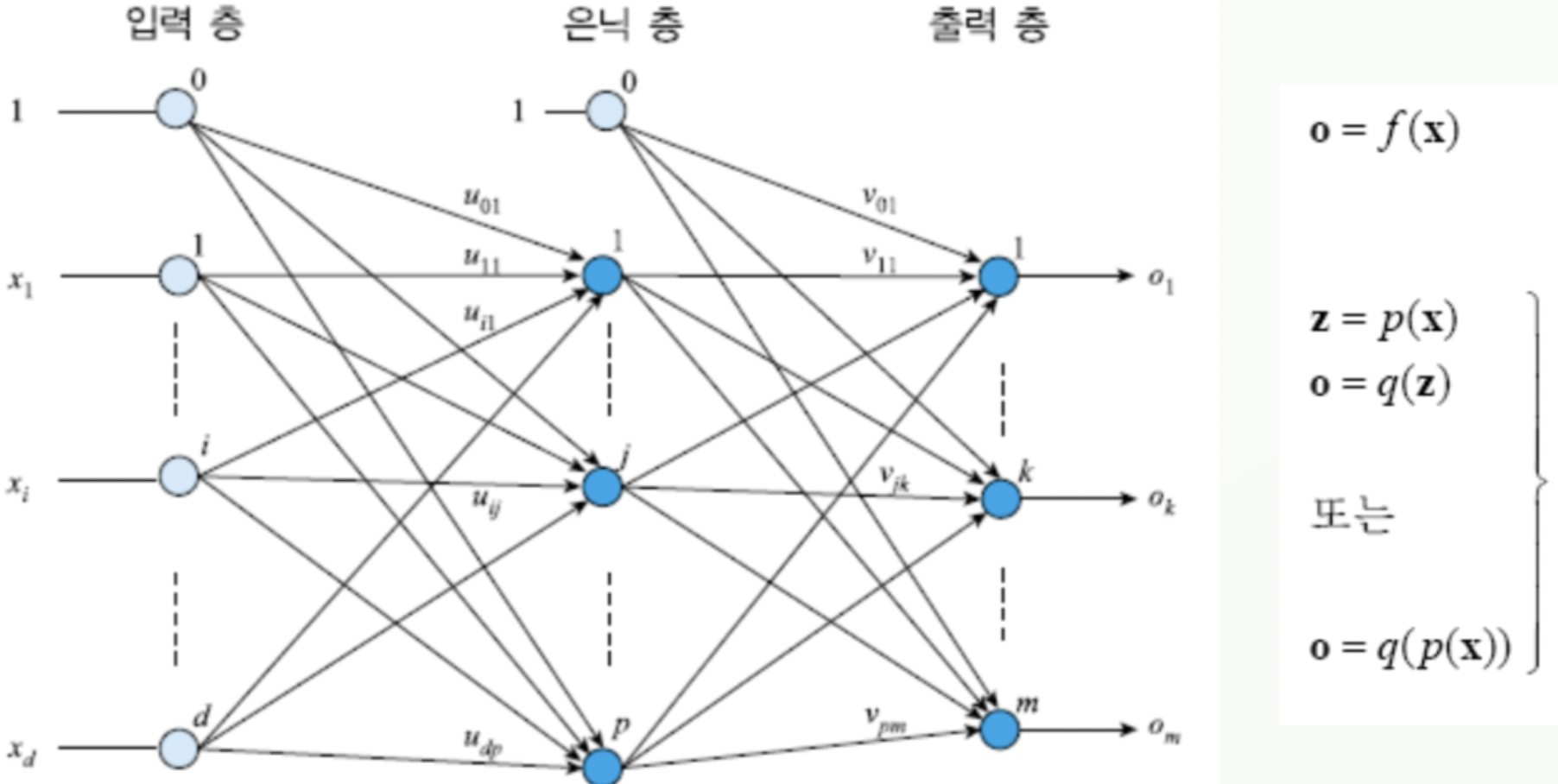
-
- 위 상황에서 입력층의 흥분에 대한 벡터
- $\mathbf x$
-
- $\mathbf x$와 가중치의 곱으로 이루어진 입력을 처리하여 결정된 은닉층의 흥분에 대한 벡터
- $\mathbf z$
-
- $\mathbf z$와 은닉층에서 뻗어나온 엣지의 가중치 곱으로 이루이진 입력을 처리하여 결정된 출력층의 흥분에 대한 벡터
- $\mathbf o$
- 입력층의 입력 $x_i$ 와 은닉층의 노드 $z_j$ 사이의 가중치 $u_{ij}$
- 은닉층의 노드 $z_j$ 와 출력층의 노드 $o_k$ 사이의 가중치 $v_{jk}$
- 수식으로 만들면
-
은닉층의 j번째 노드의 흥분여부 $z_j$의 결정
\[\left. { \begin{matrix} z\_\mathrm{sum}_j = \sum^{n}_{i=1}x_iu_{ij} + u_{0j}\\ \\ z_j = \tau(z\_\mathrm{sum}_j)\end{matrix}}\right\rbrace\] -
출력층의 k번째 노드의 흥분여부 $o_k$의 결정
\[\left. { \begin{matrix} o\_\mathrm{sum}_k = \sum^{p}_{j=1}z_jv_{jk} + v_{0k}\\ \\o_k = \tau(o\_\mathrm{sum}_k)\end{matrix} } \right \rbrace\]
-
-
- 활성 함수
- 미분 가능한 sigmoid 함수를 사용한다.
-
이진 시그모이드 함수 [0, 1]
\[\left. {\begin{matrix} \tau(x) &=& \frac{1}{1+e^{-ax}} \\ \\ \tau'(x) &=& a\tau(x)(1-\tau(x)) \end{matrix}}\right\rbrace\]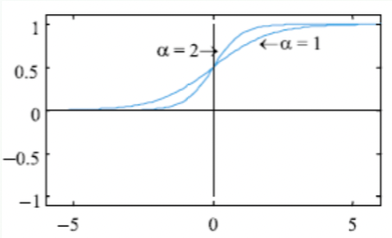
-
양극 시그모이드 함수 [-1, 1]
\[\left. {\begin{matrix} \tau(x) &=& \frac{2}{1+e^{-ax}} -1 \\ \\\tau'(x) &=& \frac a 2(1+\tau(x))(1-\tau(x))\end{matrix}}\right\rbrace\]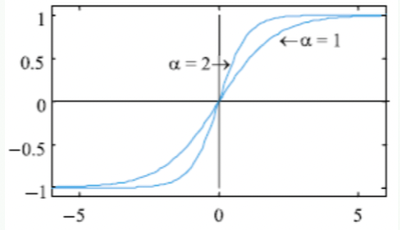
- 개요
- MLP학습
- 개요
- 훈련집합 $X=\lbrace\mathbf{(x_1,t_1),(x_2,t_2),…,(x_N,t_N)\rbrace}$이 주어졌을 때 이들을 분류한느 다층 퍼셉트론의 해 $\Theta=\lbrace\mathbf{u,v}\rbrace$ 를 찾는 것을 목표로 하는 학습. (이 때 $\mathbf{x_i}$는 특징 벡터, $\mathbf{t_i}$는 분류 표지벡터)$\begin{cases} \mathrm{t_i} = (0,…,1,…,0)^T & \ 결정함수=이진\ \mathrm{sigmoid} \ \ \mathrm{t_i} = (-1,…,1,…,-1)^T & \ 결정함수=양극\ \mathrm{sigmoid} \end{cases}$
-
패턴 인식에서 학습 알고리즘 설계과정
단계 1: 분류기 구조 정의와 분류 과정의 수학식 정의
단계 2: 분류기 품질 측정용 비용함수 $\mathrm{J}(\Theta)$정의 $(\ 매개변수\ 집합\ \Theta = \lbrace\mathbf{w}^T, b\rbrace\ )$
단계 3: $\mathrm{J}(\Theta)$를 최적화 하는 $\Theta$를 찾는 알고리즘 설계
- 예시
- 단계 1
- 분류기 식:
-
은닉층의 j번째 노드의 흥분여부 $z_j$의 결정
\[\left. \begin{matrix} z\_\mathrm{sum}_j = \sum^{n}_{i=1}x_iu_{ij} + u_{0j}\\ \\ z_j = \tau(z\_\mathrm{sum}_j)\end{matrix} \right\rbrace\] -
출력층의 k번째 노드의 흥분여부 $o_k$의 결정
\[\left. \begin{matrix} o\_\mathrm{sum}_k = \sum^{p}_{j=1}z_jv_{jk} + v_{0k}\\ \\o_k = \tau(o\_\mathrm{sum}_k)\end{matrix} \right\rbrace\]
-
- 매개변수 집합: $\Theta=\lbrace\mathbf{u,v}\rbrace$
- $\mathbf{u}$: 은닉층으로 향하는 엣지들의 가중치 집합
- $\mathbf{v}$: 출력층으로 향하는 엣지들의 가중치 집합
- 분류기 식:
-
단계 2
비용함수: $E=\frac12\sum^m_{k=1}(t_k-o_k)^2$
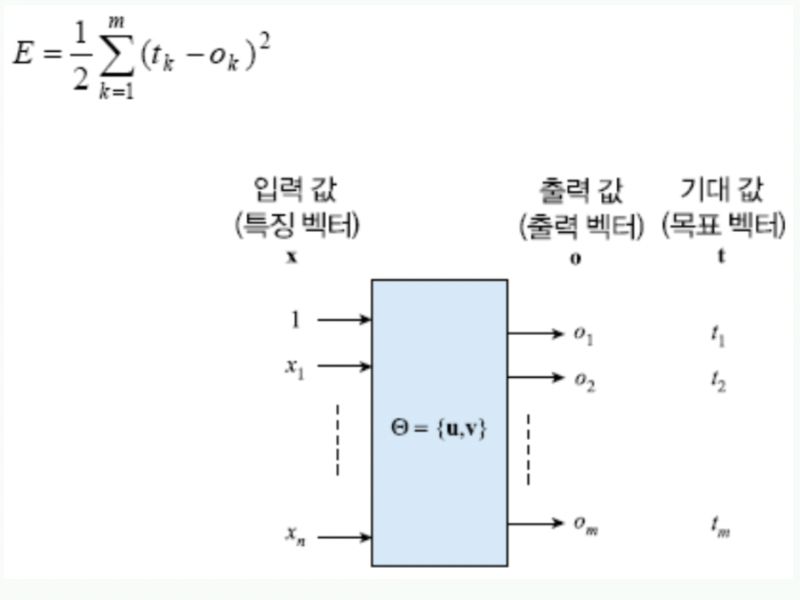
- 단계 3
-
$\mathbf{v_{jk}}$업데이트를 위한 $\Delta\mathbf{v_{jk}}$ 산출
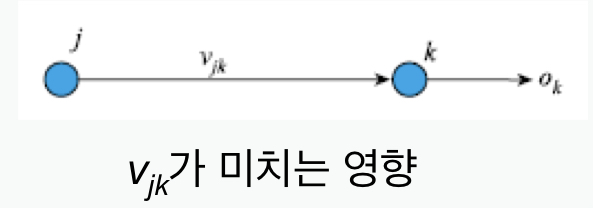
$\begin{matrix}\frac{\theta E}{\theta\mathbf{v_{jk}}}&=&\frac{\theta\ (\sum^m_{r=1}(t_r-o_r)^2)}{\theta \mathbf{v_{jk}}}\\ &=&-(t_k-o_k)\frac{\theta\ o_k}{\theta\mathbf{v_{jk}}}\\&=& -(t_k-o_k)\frac{\theta\ \tau(o_sum_k)}{\theta\mathbf{v_{jk}}}\\&=&-(t_k-o_k)\tau’(o_sum_k)\frac{\theta\ o_sum_k}{\theta\mathbf{v_{jk}}}\\&=&-(t_k-o_k)\tau’(o_sum_k)\mathrm{z}_j\end{matrix}$
$\left({0\le j \le p,\ \ \ 1\le k\le m}\right)$
$\left({\tau = \mathrm{sigmoid\ function}}\right)$
$\left({Z_j = {\theta\mathbf{v_{jk}}},\ \ \ \delta_k=(t_k-o_k)\tau’(o_sum_k)=(t_k-o_k)\frac{a}{2}(1-o_sum_k^2)}\right)$
$\therefore \Delta\mathbf{v_{jk}} = -\rho\frac{\theta E}{\theta\mathbf{v_{jk}}}=\rho\delta_k\mathrm{z}_j$
-
$\mathbf{u_{jk}}$업데이트를 위한 $\Delta\mathbf{u_{jk}}$ 산출
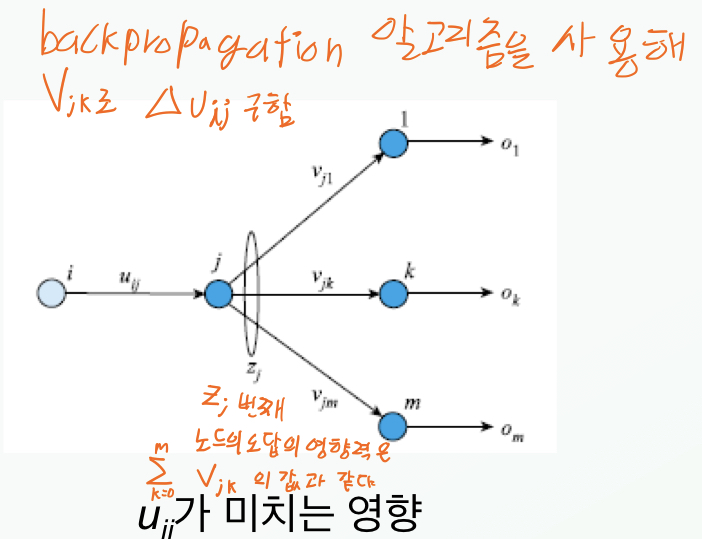
과정 생략…
\[\therefore \Delta\mathbf{u_{jk}} = -\rho\frac{\theta E}{\theta\mathbf{u_{ij}}}=\rho\eta_j\mathrm{x}_i\] \[\left({\mathrm{x}_j = \frac{1}{\theta\mathbf{u_{jk}}} ,\ \ \ \eta_j=\tau'(z\_sum_k)\sum^m_{k=1}\delta_k\mathbf{v}_{jk}}\right)\]
-
- 단계 1
- 예시
- Back Propagation Algorithm
-
$\mathrm{u}$ 와 $\mathrm{v}$ 를 초기화한다.
-
bias: $x_o=z_0=1$
-
$X$의 샘플 각각에 대해 다음을 실행한다.
3-1 현재 샘플을 $\mathrm{x}=(x_1, x_2, …x_d)^T와\ \mathrm{t}=(t_1, t_2, …t_m)^T$ 으로 표기한다.
3-2 전방계산 파트
3-2-1 $\mathrm{for}(j=1\ \mathrm{to}\ p)\ \ \lbrace\ \ \mathrm{z_sum}j=\sum^d{i=0}x_iu_{ij}; \ \ \ \mathrm{z}_j=\tau(\mathrm{z_sum}_j);\ \ \rbrace$
3-2-2 $\mathrm{for}(k=1\ \mathrm{to}\ m)\ \ \lbrace\ \ \mathrm{o_sum}k=\sum^p{j=0}z_jv_{jk}; \ \ \ \mathrm{o}_k=\tau(\mathrm{o_sum}_k);\ \ \rbrace$
3-3 오류역전파 파트
3-3-1 $\mathrm{for}(k=1\ \mathrm{to}\ m)\ \ \delta_k = (\mathrm{t}_k - \mathrm{o}_k)\tau'(\mathrm{o\_sum}_k)\ ;$ 3-3-2 $\mathrm{for}(\ \ 모든 \mathrm{v}_{jk},\ \ 0\leq j\leq p,\ \ 1\leq k\leq m에\ 대해\ )\Delta\mathrm{v}_{jk} = \rho\delta_kz_j\ ;$ 3-3-3 $\mathrm{for}(j=1\ \mathrm{to}\ p)\ \ \ \eta_j=\tau'(\mathrm{z\_sum}_j)\sum^m_{k=1}\delta_k\mathrm{v}_{jk}\ ;$ 3-3-4 $\mathrm{for}(\ 모든 \ \mathrm{u}_{ij}, 0\leq i\leq d,\ \ 1\leq j\leq p\ 에\ 대해\ )\ \ \Delta \mathrm{u}_{ij} = \rho\eta_jx_i\ ;$3-4 가중치 갱신 파트
3-4-1 $\mathrm{for}(\ 모든 \ \mathrm{u}_{ij}, 0\leq i\leq d,\ \ 1\leq j\leq p\ 에\ 대해\ )\ \ \mathrm{u}_{ij}= \mathrm{u}_{ij}+\Delta \mathrm{u}_{ij} \ ;$ 3-4-2 $\mathrm{for}(모든\ \mathrm{v}_{jk},\ 0\leq j\leq p,\ 1\leq k\leq m\ 에\ 대해\ )\ \ \mathrm{v}_{jk} = \mathrm{v}_{jk}+\Delta\mathrm{v}_{jk}\ ;$ -
3번의 시행 전체를 stop-condition (최대 epoch 도달 or 오류율 < 0) 달성까지 반복한다.
-
$\mathrm{u}$ 와 $\mathrm{v}$ 를 저장한다.

-
- 개요

There are currently no comments on this article
Please be the first to add one below :)
내용에 대한 의견, 블로그 UI 개선, 잡담까지 모든 종류의 댓글 환영합니다!!