릴레이션의 구성
-
릴레이션 예시
릴레이션 $\simeq$ 테이블
ex) 학생 릴레이션
학번 이름 학년 학과 100 나영수 4 컴공 200 이비자 3 전전 300 강이수 1 컴공 400 마동석 4 컴공 500 박종길 2 산공
도메인 (domain)
애트리뷰트가 쥐할 수 있는 값들의 집합 <- 애트리뷰트의 타입을 가리키는 의미로 자주 사용된다.
상기 예시에선
DSNO(INTEGER), NAME(CHAR(10)), YEAR(INTEGER), DEPT(CHAR(6))
$D_1, D_2, D_3, D_4$ 에 각각 대응시킬 수 있다.
-
단순 도메인 (simple domain)
분할할 수 없거나 분할하면 의미가 없어지는 값을 갖는 도메인 (원자 값)
ex) 정수, String … -
복합 도메인
분할하여도 의미를 갖는 도메인 (복합 값)
ex) 날짜 -> 연, 월, 일
애트리뷰트 (attribute)
도메인의 역할 이름 ($\simeq$ 의미)
상기 예시 에선
학번, 이름, 학년, 학과
릴레이션 스키마 (relation schema)
애트리뷰트의 집합이다.
정적인 속성을 띈다.(시간에 무관하다.)
상기 예시의 학생 릴레이션을 R 이라고 했을 때,
각 에트리뷰트를 학번 애트리뷰트는 $\mathrm{A}_1$ , 이름 애트리뷰트는 $\mathrm{A}_2$ , 학년 애트리뷰트는 $\mathrm{A}_3$ , 학과 애트리뷰트는 $\mathrm{A}_4$ 라고 할 수 있다.
R 의 릴레이션 스키마는 다음과 같이 표현할 수 있다. $\mathrm{R}(A_1, A_2, A_3, A_4)$
릴레이션 인스턴스 (relation instance)
어느 한 시점에 릴레이션 R 이 포함하고 있는 튜플들의 집합이다.
튜플의 표현: $<V_1, V_2, V_3, V_4> \ \ \ ( V_i \in D_i) $
스키마와 반대로 동적인 성질을 가지며, 시간에 따라 상태가 변한다.
릴레이션
위 내용을 바탕으로 다시 릴레이션을 정의하자면
릴레이션 = 릴레이션 스키마 + 릴레이션 인스턴스
릴레이션 R의 애트리뷰트 도메인들의 카티션프로덕트 집합의 원소 는 튜플의 해공간? 이라고 할 수 있겠다.
n개의 애트리뷰트를 갖는 릴레이션의 튜플을 n-튜플이라고 한다.
$<d_1, d_2, d_3, …, d_n >$
-
릴레이션의 차수(degree)
릴레이션의 애트리뷰트 개수
-
릴레이션의 카디날리티(cardinality)
릴레이션 튜플의 갯수
-
릴레이션의 몇 가지 특징
-
튜플의 유일성
릴레이션은 튜플의 집합(Set)이다. 당연히 원소에 중복이 있을 수 없다.
-
튜플의 무순서성
위와 같은 이유로 원소들이 순서를 가질 수 없다.
-
애트리뷰트의 무순서성
릴레이션 스키마는 애트리뷰트의 집합이다. 따라서 애트리뷰트에도 순서가 있을 수 없다.
-
애트리뷰트의 원자성
애트리뷰트값은 단일한 값을 가져야 한다. 복수의 값을 가질 수 없다. (같은 도매인을 갖는 다른 애트리뷰트가 2개 일지언정(ex. 전화번호1, 전화번호2))
널(NULL) 값도 원자로 취급된다.
-
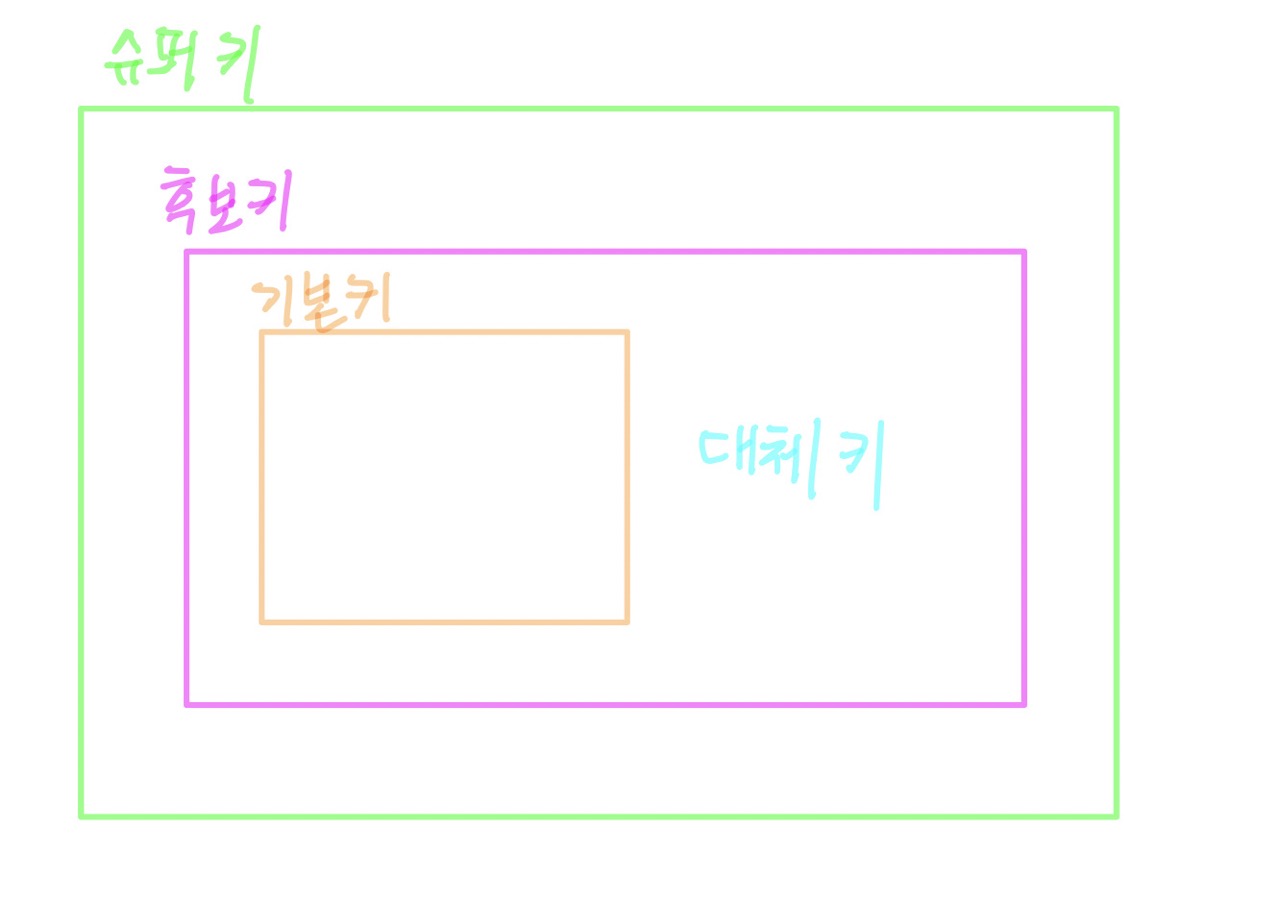
릴레이션 키
유일성 을 만족하는 키: 튜플 중 해당 키값이 동일한 튜플이 없다면 유일성 만족 (키의 기본 조건이다.)
최소성 을 만족하는 키: 키에 포함된 애트리뷰트의 갯수가 최소인 키 (최소라고 항상 1개인 것은 아니다.)
-
슈퍼 키 (super key)
유일성은 보장되지만, 최소성은 보장되지 않는 애트리뷰트의 집합
슈퍼 키의 애트리뷰트는 1개 일 수도 복수일 수도 있다.
-
후보 키 (candidate key)
유일성과 최소성을 모두 만족하는 키
-
기본 키 (primary key)
후보 키 중에서 테이터베이스의 대표로 지정된 하나의 키
각 튜플에 대해 항상 유효한 값을 가져야 한다. NULL값은 허용되지 않음
-
대체 키 (alternate key)
후보 키 중에서 기본 키를 제외한 나머지 후보 키
-
외래 키 (foreign key)
릴레이션 R의 애트리뷰트(집합) FK 가 릴레이션 S의 기본키를 가리킬 때, FK는 R의 외래키이다.
FK의 값은 S의 기본키에 존재하는 값이거나 null값이어야 한다.(null 일지언정 제 3의 값을 가져선 안된다.)
R과 S가 같은 릴레이션일 수도 있다.
이 때 R을 참조 릴레이션(referencing relation), S를 피참조 릴레이션(referenced relation)이라고 한다.
무결성 제약
-
개체 무결성: 기본키의 조건
기본 키 값은 언제나 null값을 가질 수 없고, 중복되어서도 안된다.
-
참조 무결성: 외래키의 조건
외개키 값은 반드시 피참조 릴레이션의 기본 키값으로 존재하는 값이거나 null이어야 한다.
-
도메인 무결성(domain integrity)
애트리뷰트의 값이 해당 도메인에 속한 값이어야 한다는 규정. (뻐꾸기알 꺼ㅈ)
위 세가지 무결성 제약조건은 데이터베이스 상태가 항상 만족시켜야 될 제약조건이다 !!
관계 대수
-
폐쇄 성질
피연산자와 연산 결과가 모두 릴레이션.
중첩된 수식의 표현 가능 $(\mathrm{ex.} R\times S \bowtie T )$
집합연산자
릴레이션 R, S를 예시로 설명
-
합집합 (UNION, $\cup$ )
$ R\cup S = \lbrace t |\ t \in R\ \lor\ t \in S \rbrace $
$|R\cup S| \le |R| + |S|$ ($ |R| $ 은 R의 카디날리티)
-
외부 합집합 (outer-union, $\cup^+$)
합병가능하지 않은 릴레이션간의 합집합
(합병가능한: 1. 애트리뷰트 수가 같고, 2. 대응되는 도메인이 같아야한다.)
연산 결과로 나오는 릴레이션의 애트리뷰트 값이 없을 때는 NULL값으로 채운다.
ex.
R
학번 이름 학년 100 나영수 4 300 강이수 1 500 박종길 2 S
학번 학년 학과 100 4 컴공 200 3 전전 300 1 컴공 $R\cup^+ S$
학번 이름 학년 학과 100 나영수 4 300 강이수 1 500 박종길 2 100 4 컴공 200 3 전전 300 1 컴공 -
-
교집합 (intersect, $\cap$ )
$R\cap S = \lbrace t |\ t \in R\ \land\ t \in S \rbrace $
$|R\cap S| \le \min\lbrace |R| + |S|\rbrace $
-
차집합 (difference, - )
$R- S = \lbrace t |\ t \in R\ \land\ t \notin S \rbrace $
$ |R - S| \le |R| $
-
카티션 프로덕트 (cartesian product, $\times$)
$ R\times S = \lbrace r\cdot s |\ r \in R\ \land\ s \in S \rbrace $ $ \cdot $ : 투플의 접합(concatenation) $ |R \times S| = |R| \times |S| $ $R\times S$ 의 차수(degree) = R의 차수 + S의 차수
순수 관계 연산자
-
들어가기 전에
-
릴레이션 스키마 $R(X) = R(A_1, \dots , A_n)$
-
튜플 r: $ <a_1, \dots , a_n> $
$a_i$: 튜플 r에 대한 애트리뷰트 $A_i$의 값
$a_i = r.A_i = r[A_i]$
-
-
셀렉트 (select, $\sigma$)
$\sigma_{ (조건) }(R)$
-
예시
-
$\sigma_{A\theta v}(R) = \lbrace r| r \in R\ \land r.A\theta v\rbrace $
연산결과: R 튜플 중 A 값이 어떤 값 V와 $\theta$관계인 튜플로 이루어진 릴레이션
-
$\sigma_{A\theta v}(B) = \lbrace r| r \in R\ \land r.A\theta r.B\rbrace $
연산결과: R의 튜플 중 A값이 B값과 $\theta$관계인 튜플로 이루어진 릴레이션
_단, $\theta$: 비교 연산자 $\lbrace <, >, \leq, \geq, =, \neq\rbrace $
-
연산 결과는 피연산 릴레이션의 수평적 부분집합
-
-
프로젝트 (project: $\Pi$)
$X=\lbrace A_1, A_2, \dots , A_n \rbrace $ 인 릴레이션 R(X),
$Y\subseteq X$ 인 $Y=\lbrace B_1, B_2, \dots , B_m \rbrace $에 대하여$\Pi_Y(R) = \lbrace <r.B_1, \dots, r.B_m> | r\in R \rbrace $
R의 애트리뷰트 중 Y의 애트리뷰트 집합에 포함되는 애트리뷰트들의 집합
연산 결과는 피연산 릴레이션의 수직적 부분집합
연산결과 중복되는 튜플들은 제거해야 한다.
-
세타조인 (theta join, $\bowtie$)
$R(X), S(Y), A\in X, B\in Y$ 에 대해
$R\bowtie_{A\theta B}S = \lbrace r \cdot s | r\in R \land s \in S \land (r.A \ \ \theta\ \ s.B) \rbrace $- A, B: 조인 애트리뷰트
- $r \cdot s$: 접합을 의미
- $\theta$: 비교연산자 $\lbrace <, >, \leq, \geq, =, \neq\rbrace $
- 결과 차수 = R의 차수 + S의 차수
- 조인: binary operator (피연산 릴레이션 2개, 연산결과 릴레이션 1개)
두 릴레이션 R과 S의 카티션 프로덕트에서에서 $\theta$ 조건을 만족하는 투플만 모은 (카티션 프로덕트의)수평적 부분집합
카티션 프로덕트 연산 후 SELECT 연산을 한다고 이해하면 쉽다.
-
동일 조인
세타 조인에서 $\theta$가 = 인 조인의 특수한 경우
$R\bowtie_{A = B}S = \lbrace r \cdot s | r\in R \land s \in S \land (r.A \ \ =\ \ s.B) \rbrace $
예시 ${학생}\bowtie_{학번=학번}{등록}$
-
자연 조인 (natural join, $\bowtie_N$)
R(X), S(Y)의 조인 애트리뷰트가 $X\cap Y$ (이하 Z) 인 특수한 경우
\[\begin{align} R \bowtie_N S&= \lbrace <r \cdot s> [X\cup Y] \| r\in R \land s\in S \land r[Z]=s[Z]\nonumber\\ &= \Pi_{X\cup Y}(\sigma_{Z=Z} (R \times S))\nonumber \\ &= \Pi_{X\cup Y}(R\bowtie_{Z=Z}S)\nonumber \end{align}\]동일 조인의 결과에서 중복되는 애트리뷰트를 제거한 릴레이션
일반적으로 애트리뷰트 Z는 S의 외래키(동시에 R의 기본키)로 구성된다.
연결된 데이터를 두 테이블로 분리하여 보관하고, 다시 연결된 테이블이 필요할 때 자연조인으로 복원하여 사용할 수 있다.
-
세미 조인 (semijoin $\ltimes$)
$R\ltimes S$: S와 자연 조인이 가능한 R의 튜플 집합
$R\ltimes S= R\bowtie_N(\Pi_Z(S))$
좀 더 직관적인 표현
$R\ltimes S = \Pi_X(R\bowtie_N S)$자연조인의 결과 로 나오는 R과 S의 짝 말고, R 쪽만!
-
외부 조인 (outerjoin, $\bowtie^+$)
두 릴레이션을 조인할 때 상대 릴레이션에 대응되는 튜플이 없는 경우 배제하는 대신 상대의 위치에 null 튜플을 넣어 조인을 하는 것
연산 결과로 나온 릴레이션에 정보 누락이 없다.
왼쪽 외부조인(left outer join): 왼쪽의 릴레이션의 투플들에게만 관대한 조인
오른쪽 외부조인(right outer join): 오른쪽의 릴레이션 튜플들에게만 관대한 조인 -
디비전 (Division: $\div$)
릴레이션 R(X), S(Y)에 대하여
$Y\subseteq X$ 이고 $D = X - Y$ 라고 하면 $X = D\cup Y$즉, R(X) = R(D, Y), S(Y) 에 대하여
$R\div S = \lbrace t| t \in \Pi_D(R) \land t\cdot s \in R\ \ \mathrm{for\ all}\ s\in S\rbrace $
S에 있는 모든 튜플과 쌍을 이루는 R의 튜플을 구하라
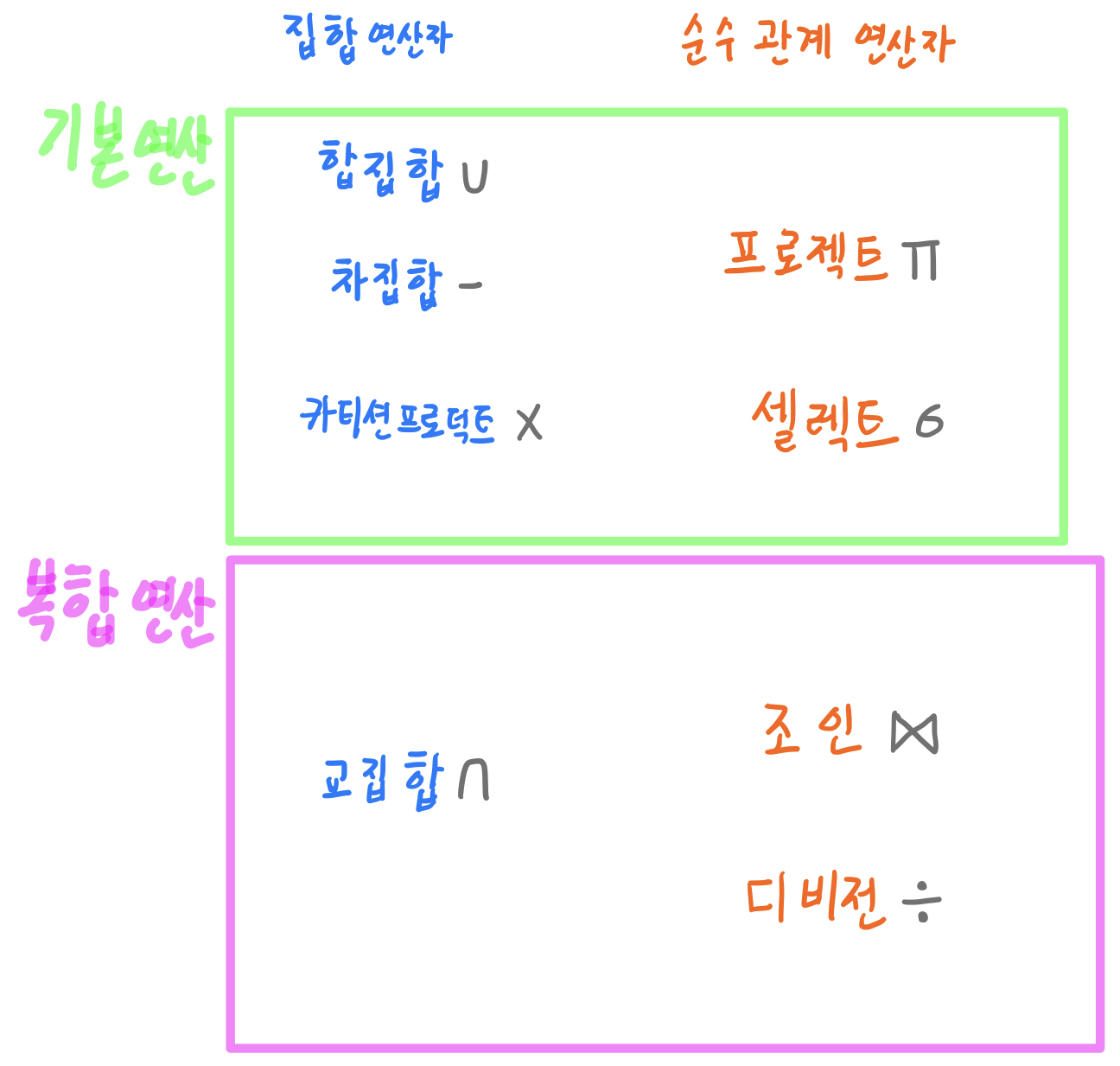
기본연산, 복합연산
-
기본연산 (primitive operations)
다른 연산으로 대체될 수 없는 하나의 논리적 기능을 수행하는 연산
합집합($\cup$), 차집합(-), 곱집합($\times$), 프로젝트($\Pi$), 셀렉트($\sigma$)
-
복합연산 (composite operations)
기본 연산의 조합으로 대체할 수 있는 연산
교집합($\cap$), 조인($\bowtie$), 디비전($\div$)
교집합
\(\begin{align} R\cap S &= R\ -\ (R\ -\ S)\ =\ S\ -\ (S\ -\ R)\nonumber\\ &= (R\cup S) - (\ (R\ -\ S)\ \cup\ (S\ -\ R))\nonumber \end{align}\)조인
$R\bowtie_{A\theta B}S = \sigma_{A\theta B}(R\times S)$디비전
$R(Z, Y) \div S(Y) = \Pi_Z(R) - \Pi_Z((\Pi_Z(R)\times S) - R)$
예제
-
다음 데이터베이스에 대한 두 질의문을 관계대수로 표현하라
Customer(cid, name, birthyear, gender)
Product(pid, name, price, category, company, pdate)
Purchase(cid, pid, pcdate)1.”Apple”사에서 제작한 상품을 하나라도 구매한 이력이 있는 ‘여성’ 고객의 이름과 구매일자를 검색하라
$\Pi_{\lbrace \mathrm{name}, \mathrm{pcdate}\rbrace}\ (\ \ (\ (\sigma_{\mathrm{gender=}\mathrm{“female”}}(\mathrm{Customer}))\bowtie_N\mathrm{Perchase})\ltimes(\sigma_{\mathrm{company}=”\mathrm{Apple}”}(\mathrm{Product}))\ \ )$
2. “Apple”사에서 제작한 모든 상품을 구매한 이력이 있는 여성고객의 이름과 생년을 검색하라
$\Pi_{\lbrace \mathrm{name, birthyear}\rbrace}( (\sigma_{\mathrm{gender=}\mathrm{“female”}}(\mathrm{Customer}))\ltime(\Pi_{\lbrace\mathrm{cid, pid}\rbrace}(\mathrm{purchase})\div\Pi_{\mathrm{pid}}(\sigma_{\mathrm{company=”Apple”}}(Product))))$
-
서로 다른 두 개의 학생 테이블 S1, S2에 대하여, 관계대수 연산결과를 테이블 형태로 표현하라
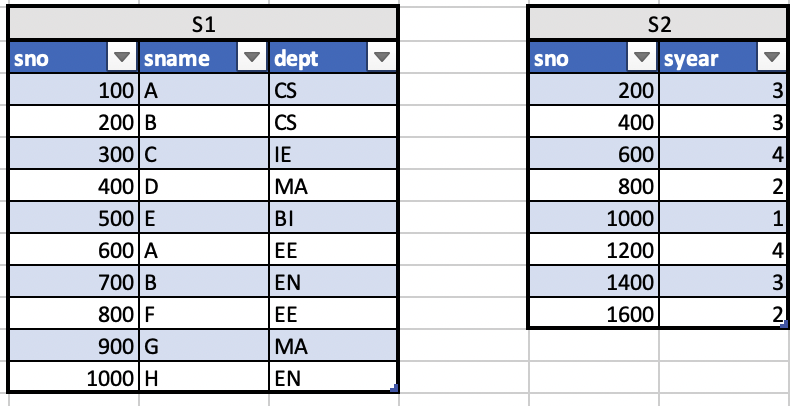
1.S1과 S2의 자연조인 결과를 구하라
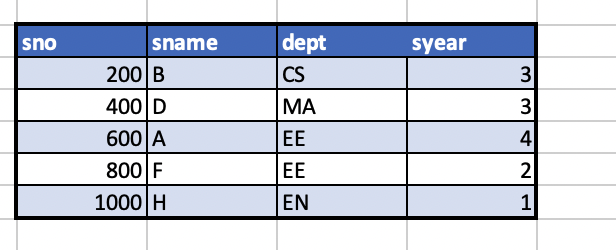
natural join
2.S1과 S2의 세미조인 결과를 구하라
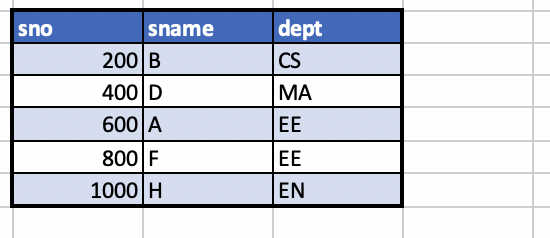
semi join
3.S1과 S2의 외부조인 결과를 구하라
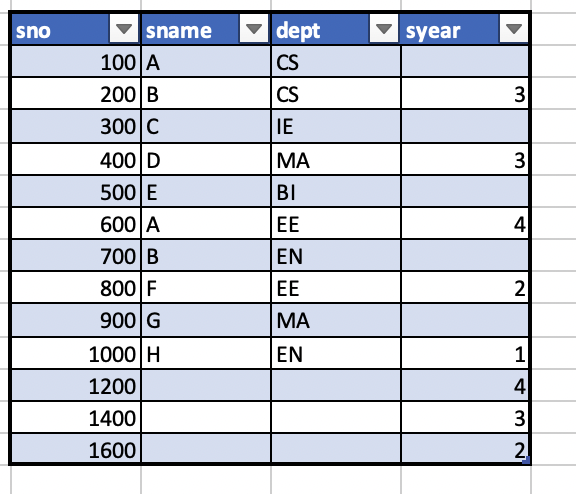
full outer join
4.S1과 S2의 왼쪽외부조인 결과를 구하라
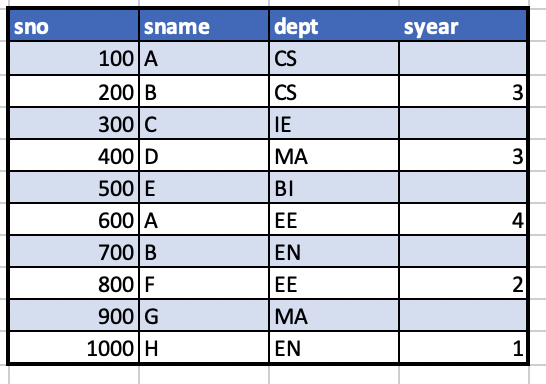
left outer join
5.S1과 S2의 외부합집합 결과를 구하라
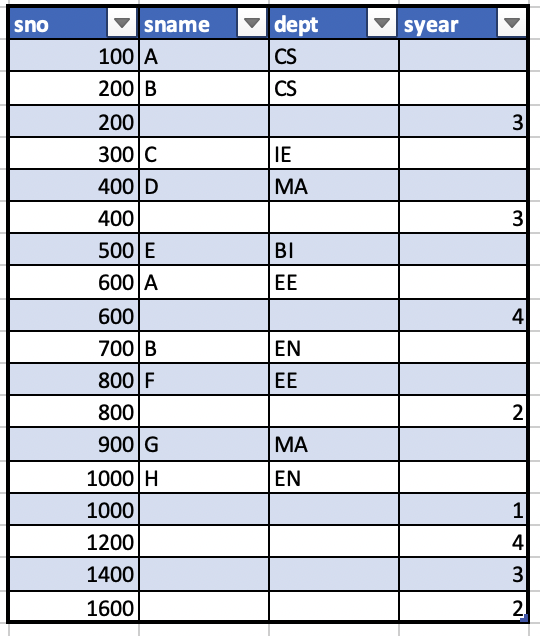
outer union

There are currently no comments on this article
Please be the first to add one below :)
내용에 대한 의견, 블로그 UI 개선, 잡담까지 모든 종류의 댓글 환영합니다!!